Un article de Wikipédia, l'encyclopédie libre.
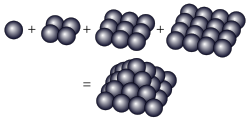 Nombre pyramidal carré : 1+4+9+16=30.
Nombre pyramidal carré : 1+4+9+16=30.
En arithmétique géométrique, un nombre pyramidal est un nombre figuré polyédrique représenté par une pyramide dont la base, un polygone régulier, représente un nombre polygonal. La pyramide est formée de couches représentant des nombres polygonaux successifs.
 Nombre pyramidal hexagonal : 1 + 6 + 15 + 28 = 50.
Nombre pyramidal hexagonal : 1 + 6 + 15 + 28 = 50.
Pour tous entiers  et
et  , le
, le  -ième nombre
-ième nombre  -pyramidal est donc[1] la somme des nombres
-pyramidal est donc[1] la somme des nombres  -gonaux d'indices 1 à
-gonaux d'indices 1 à  :
:

On a la relation :  [2], dont on déduit
[2], dont on déduit  ;
;
 est le
est le  -ième nombre tétraédrique.
-ième nombre tétraédrique.
| Nombre pyramidal |
Somme de |
Formule |
Les dix premiers nombres |
Numéro OEIS
|
| Nombre pyramidal triangulaire, ou nombre tétraédrique |
nombres triangulaires |
 |
1, 4, 10, 20, 35, 56, 84, 120, 165, 220 |
suite A000292 de l'OEIS
|
| Nombre pyramidal carré |
nombres carrés |
 |
1, 5, 14, 30, 55, 91, 140, 204, 285, 385 |
suite A000330 de l'OEIS
|
| Nombre pyramidal pentagonal |
nombres pentagonaux |
 |
1, 6, 18, 40, 75, 126, 196, 288, 405, 550 |
suite A002411 de l'OEIS
|
| Nombre pyramidal hexagonal |
nombres hexagonaux |
 |
1, 7, 22, 50, 95, 161, 252, 372, 525, 715 |
suite A002412 de l'OEIS
|
| Nombre pyramidal heptagonal |
nombres heptagonaux |
 |
1, 8, 26, 60, 115, 196, 308, 456, 645, 880 |
suite A002413 de l'OEIS
|
|
|---|
| Bidimensionnel |
|
| Tridimensionnel |
|
| Quadridimensionnel |
|
| Multidimensionnel |
|















