En théorie des nombres, l'écart entre nombres premiers désigne la différence entre deux nombres premiers consécutifs.

De nombreux résultats et conjectures sont liés à cet objet. Par exemple la conjecture des nombres premiers jumeaux dit que la suite des écarts entre nombres premiers prend la valeur 2 un nombre infini de fois.

Ainsi les 30 premiers écarts (suite A001223 de l'OEIS) sont :

1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, 4, 2, 4, 14.

En notant p_n le n-ième nombre premier, le n-ième écart est :

${\displaystyle g_{n}=p_{n+1}-p_{n}}$.

Ce qui permet aussi d'écrire

${\displaystyle p_{n+1}=2+\sum _{i=1}^{n}g_{i}}$.

De même que ${\displaystyle (p_{n})}$, la suite (g_n) est non bornée : si l'on note q_n le produit p₁…p_n, tous les entiers de q_n + 2 à q_n + p_n sont composés^[1].

Le premier écart, qui est à la fois le plus petit et le seul écart impair est 1, entre le seul nombre premier pair, 2, et le premier nombre premier impair, 3. Tous les autres écarts sont pairs.

(3, 5, 7) est l'unique triplet de nombres premiers consécutifs dont l'écart est 2.

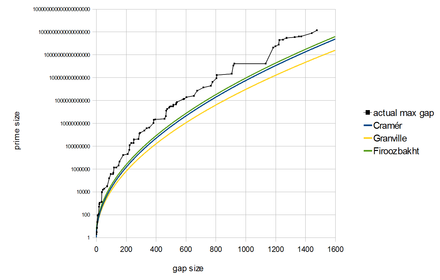
D'après le postulat de Bertrand, g_n < p_n.

Le théorème des nombres premiers suggère que g_n est^[2] asymptotiquement de l'ordre de log n, et la conjecture de Cramér pronostique un comportement en le carré du logarithme^[3]. La conjecture des nombres premiers jumeaux dit qu'elle prend la valeur 2 une infinité de fois.

L'écart le plus fréquent entre nombres premiers est d'abord 2, puis 6, et l'on conjecture que ce serait ensuite 30, 210, 2310, … c'est-à-dire les primorielles de p_n^[4].

Inégalité de Bonse

(en) Terence Tao, « Small and large gaps in the primes (slides) », avril 2015

• Arithmétique et théorie des nombres