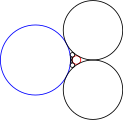
En géométrie, une chaîne de Steiner est une suite finie de cercles tangents à deux cercles fixes disjoints — les « cercles de départ » — , chacun des cercles étant en contact avec le précédent.
Les chaînes de Steiner portent le nom du mathématicien suisse Jakob Steiner (1796 - 1863)[1],[2],[3].
Un résultat fondamental est le porisme de Steiner[4], ou alternative de Steiner [5],[6], qui dit :
- Si, pour une paire de cercles de départ, le dernier cercle de la chaîne touche le premier, alors la chaîne se refermera quel que soit le premier cercle, avec le même nombre de cercles[7].
On en déduit que si une chaîne ne se referme pas, aucune ne se refermera.
Pour la construction de chaînes de Steiner, l'inversion est un outil puissant qui transforme une chaîne de Steiner en une autre chaîne de Steiner, en particulier en une chaîne de Steiner dont les cercles de départ sont concentriques. Les hexlets de Soddy sont une généralisation des chaînes de Steiner avec des sphères, et les chaînes de Pappus étudient le cas où les deux cercles de départ sont tangents[8].
Terminologie et variantes
Terminologie
Il est commode de voir une chaîne de Steiner comme formée d'une succession de cercles, appelés « cercles de Steiner », commençant par un cercle « initial » et se terminant par un cercle « final ». Habituellement, on considère des chaînes « fermées », dans lesquelles le cercle final est aussi tangent au cercle initial; sinon la chaîne est dite « ouverte ».
Quant aux cercles de départ, la seule condition est qu'ils ne se touchent pas et ne se coupent pas. Cela implique que, soit le plus petit des cercles est à intérieur du plus grand, soit les deux cercles sont à l’extérieur l'un de l’autre sans se toucher.
La figure illustre le cas d'une chaîne de Steiner fermée avec les deux cercles de départ contenus l'un dans l'autre — c'est ce qui est appelé le « cas standard » dans la suite.
Variantes
En plus du cas standard, il existe plusieurs variantes.
Chaîne fermée, ouverte ou multi-cyclique
Habituellement, on considère des chaînes de Steiner fermées, où les cercles initial et final sont tangents. Sinon, il reste un espace entre les deux cercles extrêmes (le cas d'une chaîne ouverte), et si on ajoute un cercle supplémentaire, les deux cercles extrêmes se chevauchent. En poursuivant la construction, on peut faire plusieurs tours et allonger la chaîne. Si finalement on obtient que le cercle final est tangent au cercle initial, on parle d'une chaîne multi-cyclique. L'image de droite montre une chaîne de Steiner qui fait deux tours avant de se fermer ; le premier tour est représenté par des cercles noirs, le deuxième par des disques verts. Dans ces exemples les cercles de départ sont concentriques (en couronne).
- Exemples de chaînes de Steiner fermée, ouverte, multi-cyclique
-
une chaîne fermée
-
une chaîne ouverte chevauchante
-
une chaîne multi-cyclique
Trois variantes sur la position des cercles
Les deux cercles de départ peuvent être l'un à l'intérieur de l'autre, ou à l'extérieur l'un de l'autre. Dans le deuxième cas, l'un des cercles de la chaîne peut contenir tous les autres.
- Variantes de contact
-
1. Un des cercles de départ est à l'intérieur de l’autre.
-
2. Les cercles de départ sont à l’extérieur l'un de l’autre.
-
3. Comme le cas précédent, mais de plus un des cercles de la chaîne contient tous les autres.
Ceci donne les trois variantes suivantes (dans les illustrations, les cercles de la chaîne sont en noir, les cercle initial et final en bleu et en rouge) :
- Les cercles de départ sont l’un à l'intérieur de l’autre ; les cercles de la chaîne sont tangents entre eux, et tangents aux cercles de départs ; ils sont à l'intérieur du grand cercle de départ et donc à l'extérieur du petit cercle : c'est le cas « standard ».
- Les cercles de départ sont à l'extérieur l'un de l’autre ; les cercle de la chaîne, tangents entre eux, sont tangents aux cercles de départ, mais à l'extérieur des deux.
- Les cercles de départ sont à l'extérieur l'un de l’autre ; les cercles de la chaîne sont toujours tangents entre eux et ils sont tous sauf un à l'extérieur des deux cercles de départ ; le dernier des cercles de la chaîne au contraire contient les deux cercles de départ et les autres cercles de la chaîne (dans l'exemple, sept des huit cercles de la chaîne et les cercles de départ sont à l'intérieur du huitième).
Propriétés
Porisme de Steiner

L'énoncé fondamental sur les chaînes de Steiner est la propriété appelé porisme ou alternative de Steiner[9],[6] :
Porisme de Steiner — S'il existe une chaîne de Steiner fermée pour deux cercles de départ donnés, alors il en existe une infinité, et tout cercle qui est tangent aux deux cercles de départ peut être choisi comme cercle initial d'une chaîne de Steiner fermée.
En d'autres termes, toute chaîne se déduit de l'une d'entre elles par une « rotation »[10] le long des chaînes de départ.
L'image animée illustre le théorème dans le cas d'une chaîne de six cercles dans le cas standard : les cercles de départ sont bleu et rouge.
Centres et points de contact
Les points de contact des cercles d'une chaîne de Steiner sont situés sur un cercle (de couleur or dans la figure animée) qui est le cercle bissecteur (en anglais « mid-circle »)[11].
Les centres des cercles sont sur une conique :
- Dans le cas standard, c'est une ellipse (verte dans l'animation) dont les foyers sont les centres des deux cercles de départ. Cette propriété continue à être vérifiée quand les cercles de la chaîne sont à l'intérieur d'une des cercles et à l'extérieur de l'autre, et ceci également dans les chaînes de Pappus, dans les hexlets de Soddy tridimensionnels et dans les cercles d'Apollonius ou les cas du théorème de Descartes.
- Dans l'autre cas (où les deux cercles de départ sont à l'extérieur l’un de l’autre), les centres sont sur une hyperbole.
Droites concourantes
Les tangentes aux points de contact successifs des cercles, et les droites joignant les deux points de contact de chaque cercle avec les cercles de départ sont concourantes [7].
Généralisations
- Généralisations
-
Chaîne de Pappus
-
Sextuple de Soddy
Lorsque les deux cercles de départ se touchent, on obtient une chaîne de Pappus. Les hexlets de Soddy[12] sont des chaînes de Steiner de six éléments en trois dimensions : les cercles sont remplacés par des boules. Les centres des six boules (qui forment le « sextuple ») sont dans un même plan et sont situés sur la même ellipse que les centres des cercles de la chaîne de Steiner correspondante. L'enveloppe des boules est une cyclide de Dupin (en), image par inversion d'un tore. En fait, les six boules du sextuple ne touchent pas seulement la boule de départ intérieure (en rouge) et la boule de départ extérieure, mais aussi deux autres boules (qui ne sont pas représentées dans l’animation) situées respectivement au-dessus et en dessous du plan contenant les centres du sextuple[13].
Le cas des cercles concentriques
- Chaînes de Steiner en couronnes
-
n=3 -
n=6 -
n=9 -
n=12 -
n=20

Le cas le plus simple est celui où les deux cercles de départ son concentriques. Les cercles d'une chaîne de Steiner fermée sont tous de même rayon. On note et le rayon du petit et du plus grand des cercles de départ, et le rayon des cercles de Steiner. Ces nombres sont liés par la relation . Si la chaîne est composée de cercles, l'angle entre les centres de deux cercles consécutifs est . La distance entre les centres de deux cercles consécutifs est , et la bissectrice crée deux triangles rectangles. Notons l'angle du point central ; alors . Il en résulte que :
Ceci donne l'expression pour le rayon des cercles de Steiner :
Comme , la relation entre et pour qu'une chaîne de Steiner à cercles existe est, avec , donnée par :
- .
Le critère portant sur le rapport entre les rayons s'étend à toute paire de cercles en utilisant l'écart inversif (en) des deux cercles de départ. Si ceux-ci sont concentriques, l'écart est par définition le logarithme naturel du quotient de leur rayon, soit
- .
Le critère s'écrit alors
- .
Si une chaîne de Steiner multi-cyclique contient cercles et fait tours avant de se refermer, l'angle entre deux cercles de Steiner est :
Les autres formules restent inchangées.
Le porisme de Steiner, c'est-à-dire l'affirmation que toute rotation d'une chaîne de Steiner en est encore une, est évidente dans le cas des cercles concentriques.
Le cas général
-
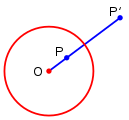
Le point P' est l’inverse du point P par rapport au centre d'inversion O; le cercle d'inversion est en rouge.
-
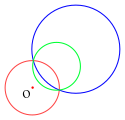
L'inverse du cercle en bleu est le cercle en vert et réciproquement.
Le cas général se ramène au cas de deux cercles concentriques par l'emploi d'un outil puissant qui est l'inversion dans le plan. Les propriétés générales des inversions qui servent ici sont :
- Un cercle qui ne passe pas par le centre d'inversion est transformé en un cercle qui ne passe pas par le centre d'inversion.
- Deux cercles tangents restent tangents après inversion.
- Les centres d'un cercle et de son inverse sont alignés avec le centre d'inversion.
La propriété de l’inversion qui intervient ici est :
- L'inversion transforme une chaîne de Steiner en une autre chaîne avec le même nombre de cercles.
Pour la preuve de l’existence, on utilise la propriété suivante qui permet de ramener le cas général au cas de cercles concentriques[14] :
- Deux cercles qui ne s'intersectent pas peuvent être transformés, par inversion, en deux cercles concentriques.
Chaînes conjuguées
- Chaînes de Steiner conjuguées à 4 cercles de Steiner
-
Une chaîne de Steiner avec les cercles de départ en rouge et bleu.
-
Le même ensemble de cercles, avec un autre choix des cercles de départ.
-
Le même ensemble de cercles, avec encore un autre choix des cercles de départ.
Si une chaîne de Steiner est composée 4 cercles, deux cercles opposés de la chaîne peuvent être choisis comme cercles de départ d'une nouvelle chaîne ; les cercles de départ de la chaîne originale deviennent éléments de la nouvelle chaîne. Ceci peut être généralisé à une des chaînes de Steiner ayant un nombre pair d'éléments, en la décomposant en plusieurs chaînes.
Articles connexes
- Chaîne de Pappus
- Grand théorème de Poncelet
- Théorème de Descartes
- Cercles d'Apollonius
- Empilement compact
- Hexlet de Soddy
Notes et références
- ↑ Ogilvy 1990
- ↑ Coxeter et Greitzer 1997
- ↑ Daniel 1993
- ↑ Un porisme est un énoncé qui relie le nombre de solutions d'un problème. En géométrie, il décrit une figure qui existe seulement si une certaine condition est remplie, dans quel cas il y a une infinité de solutions.
- ↑ Marcel Berger, Géométrie, t. 1, Cassini, , p. 362-363, n°10.10.3
- Daniel Perrin, Un projet de livre de géométrie projective (lire en ligne), p. 98-103
- David Wells, Le dictionnaire Penguin des curiosités géométriques, Eyrolles, , p. 237
- ↑ Ogilvy, p. 60.
- ↑ Coxeter et Greitzer 1997, p. 146
- ↑ Ce ne sont pas des rotations usuelles, puisque la taille change aussi !
- ↑ Coxeter et Greitzer 1997, p. 143-145
- ↑ Ogilvy 1990, chapitre 5
- ↑ (en) Bob Allanson, « Soddy's Hexlet » (consulté le ).
- ↑ Coxeter et Greitzer 1997, Th. 5.71
Bibliographie
- (en) Charles Stanley Ogilvy, Excursions in Geometry, New York, Dover, , vi+178 (ISBN 0-486-26530-7, présentation en ligne), p. 51–54
- Harold Scott MacDonald Coxeter et Samuel L. Greitzer (trad. de l'anglais), Redécouvrons la géométrie, Paris, Éditions Jacques Gabay, , 211 p. (ISBN 2-87647-134-5)Réimpression de la traduction française, parue chez Dunod en 1971, de l'ouvrage publié en 1967 en langue anglaise sous le titre Geometry revisited.
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-91-635208-4)
- Jean-Claude Daniel, « Les porismes de Steiner », Repères, IREM, no 11, , p. 33-46 (lire en ligne)
Liens externes
Animations
- Alexander Bogomolny: Steiner's Chain: What is it? (Applette Java interactive)
- Michael Borcherds: Steiner's Chain (Applette Java interactive)
- Bob Allanson: Steiner's Porism (Applette Java interactive)
- Bob Allanson: Soddy's Hexlet (Applette Java interactive)
- http://codepen.io/yukulele/pen/OVOEdX/ Animation interactive sur Codepen
Documentation
- (en) Eric W. Weisstein, « Steiner chain », sur MathWorld
- (en) Eric W. Weisstein, « Steiner's Porism », sur MathWorld