La chiralité (du grec χείρ, kheir : main) est une importante propriété reliant les notions de symétrie et d'orientation, intervenant dans diverses branches de la science.

Un objet ou un système est appelé chiral s’il n'est pas superposable à son image dans un miroir. Cet objet et son image miroir constituent alors deux formes différentes qualifiées d'énantiomorphes (du grec formes opposées) ou, en se référant à des molécules, des conformations spatiales « gauches » et « droites » appelées énantiomères dotés d'une asymétrie moléculaire tridimensionnelle. Le groupe des isométries laissant globalement invariant l'objet initial ne possède que des rotations.

Un objet (ou une molécule) non chiral est dit achiral (ou parfois amphichiral). Il est superposable à son image miroir. Autrement dit, le groupe des isométries laissant globalement invariant l'objet possède au moins une isométrie indirecte.

La chirogenèse est la formation de molécules chirales.

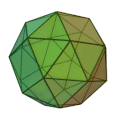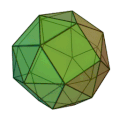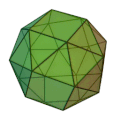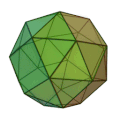
En mathématiques, un polyèdre est chiral s'il n'est pas superposable à son image par réflexion. Un objet chiral et son image miroir sont dits être énantiomorphes. Le mot chiralité est dérivé du grec χείρ (kheír), la main, l'objet chiral le plus familier; le mot énantiomorphe est formé à partir des mots grecs ἐναντίος (enantíos) 'opposé' et μορφή (morphe) 'forme'. Une figure non chirale est appelée achirale. Si un polyèdre est chiral, il possède deux formes énantiomorphes : une lévogyre (« qui tourne à gauche », en latin lævus : gauche) et une dextrogyre (« qui tourne à droite », en latin dexter : droit), comme les deux cubes adoucis ci-dessous.

• 
  Le cube adouci (sens anti-horaire)
• 
  Le cube adouci (sens horaire)

Plus formellement, une figure est achirale si et seulement si son groupe de symétrie contient au moins une isométrie indirecte. En géométrie euclidienne, toute isométrie peut être écrite comme une application ${\displaystyle v\mapsto Av+b}$ avec une matrice orthogonale ${\displaystyle A}$ et un vecteur ${\displaystyle b}$. Le déterminant de ${\displaystyle A}$ est alors soit 1 ou -1. Si c'est -1, l'isométrie est indirecte. Une telle isométrie inverse l'orientation de l'espace, sinon elle est dite directe et est une matrice de rotation.

Il existe une définition mathématique générale de la chiralité dans les espaces métriques, qui ne sont pas supposés être euclidiens ni orientables. Elle s'appuie sur l'existence ou non d'une isométrie indirecte (qui ne peut pas s'écrire comme un produit de carrés d'isométries) laissant invariant l'objet^[1].

La chiralité peut être comparée à un simple problème de gants. Tous les enfants ont déjà été confrontés à un problème de chiralité en mettant la main droite dans le gant gauche et inversement. Un gant est un objet chiral car il n'est pas superposable à son image dans un miroir. Tout comme les pieds.

La distribution d'éléments différents dans l'espace, par exemple autour d'un point, peut conduire à des situations non identiques, donc des objets différents. Ainsi les dés à jouer sont des objets chiraux : la règle de construction veut que la somme des faces opposées soit égale à sept. Posons le six sur la face supérieure et par conséquent le un sur la face inférieure, puis le cinq devant donc le deux derrière. Il reste deux façons non équivalentes de terminer : le quatre à gauche et le trois à droite, ou inversement. On obtient deux formes énantiomorphes images l'un de l'autre dans le miroir.

L’hélice (et par extension les cordes/ficelles tournées, pas de vis, tire-bouchons, poignées de porte, etc) et le ruban de Möbius, de même que les tétrominos de forme S et Z du jeu vidéo populaire Tetris, montrent aussi la chiralité, bien que ces derniers soient seulement en deux dimensions.

Beaucoup d’autres objets familiers montrent la même symétrie chirale du corps humain (ou énantiomorphe) — gants, verres, chaussures, jambes d'une paire de bas, ciseaux, guitare, etc. — Une notion de chiralité similaire est considérée en théorie des nœuds, comme expliqué ci-dessous. Ou encore en biochimie pour la conformation et la réplication des protéines et pour expliquer le comportement pathogène et difficile à traiter de certains virions ou de maladies auto-immunes, et en physique subnucléaire pour les phénomènes de spin.

En trois dimensions, chaque figure qui possède un plan de symétrie ou un centre de symétrie est nécessairement achirale, puisque la réflexion par rapport à ce plan, ou la symétrie centrale selon le centre de symétrie sont des isométries indirectes laissant globalement invariante la figure :

• Un plan de symétrie d'une figure ${\displaystyle F}$ est un plan ${\displaystyle P}$, tel que ${\displaystyle F}$ est invariant avec l’application ${\displaystyle (x,y,z)\mapsto (x,y,-z)}$, lorsque ${\displaystyle P}$ est choisi comme étant le plan ${\displaystyle x}$-${\displaystyle y}$ du système de coordonnées.
• Un centre de symétrie d’une figure ${\displaystyle F}$ est un point ${\displaystyle C}$, tel que ${\displaystyle F}$ est invariant par l’application ${\displaystyle (x,y,z)\mapsto (-x,-y,-z)}$, lorsque ${\displaystyle C}$ est choisi comme étant l’origine du système de coordonnées).

Il existe néanmoins des figures achirales qui manquent de plan et/ou de centre de symétrie. Un exemple est la figure :

${\displaystyle F_{0}=\left\{(1,0,0),(0,1,0),(-1,0,0),(0,-1,0),(2,1,1),(-1,2,-1),(-2,-1,1),(1,-2,-1)\right\}}$

qui est invariante sous l’isométrie de renversement d’orientation ${\displaystyle (x,y,z)\mapsto (-y,x,-z)}$ ; elle est donc achirale, mais ne possède ni plan de symétrie, ni centre de symétrie.

La figure

${\displaystyle F_{1}=\left\{(1,0,0),(-1,0,0),(0,2,0),(0,-2,0),(1,1,1),(-1,-1,-1)\right\}}$

est également achirale ; elle a l’origine pour centre de symétrie, mais elle n'a pas de plan de symétrie.

En deux dimensions, chaque figure qui possède un axe de symétrie est achirale, et il peut être montré que chaque figure achirale bornée doit avoir un axe de symétrie. (Un axe de symétrie d'une figure ${\displaystyle F}$ est une droite ${\displaystyle L}$, tel que ${\displaystyle F}$ est invariante par l'application ${\displaystyle (x,y)\mapsto (x,-y)}$, lorsque ${\displaystyle L}$ est choisie comme étant l'axe ${\displaystyle x}$ du système de coordonnées).

Considérons le motif suivant :

< < < < < < < < < <
 < < < < < < < < < <

Cette figure est chirale, elle n’est pas identique à son image miroir suivant un axe ou l’autre :

 < < < < < < < < < <
< < < < < < < < < <

 > > > > > > > > > >
> > > > > > > > > >

Mais, si on prolonge le motif dans deux directions vers l'infini, on récupère une figure achirale (non-bornée) qui ne possède pas d'axe de symétrie. Son groupe de symétrie est un groupe de frise engendré par une réflexion glissée.

Un nœud est dit achiral (ou amphichiral) s’il peut être déformé continument en son image miroir ; sinon, il est dit chiral (en). Par exemple, le nœud trivial et le nœud de huit (en) sont achiraux, alors que le nœud de trèfle est chiral.

Un champ vectoriel a la symétrie miroir : Exemple : le champ électrique produit par un « électron miroir » est l'image dans le miroir du champ produit par l'électron. En revanche le champ magnétique produit par le mouvement de l'« électron miroir » est inversé : le champ magnétique Bm derrière le miroir s'obtient en prenant l'antisymétrique du champ B devant le miroir. Cela provient de la définition du champ magnétique par un produit vectoriel ; le produit vectoriel n'est pas un vecteur, mais un tenseur antisymétrique qui ne comporte que trois composantes non nulles dans un espace à trois dimensions et qui peut donc être représenté par trois composantes : un pseudo-vecteur.

Les lois fondamentales de la physique doivent être achirales, sauf l'interaction faible, qui n'est pas invariante dans la symétrie miroir, sauf à remplacer les particules par leurs antiparticules ; et la désintégration du kaon semble ne pas vérifier cette symétrie.

La chiralité est importante en physique des particules du fait que l'univers est asymétrique pour les spins.

Or jusqu'à présent, les neutrinos détectés ont une hélicité gauche (valeur de spin projeté sur la direction du mouvement = -1/2 < 0 ) et les antineutrinos une hélicité droite (valeur de spin projeté sur la direction du mouvement = +1/2 > 0) ; on peut comprendre cette rupture de la parité (invariance pour l'inversion du système de coordonnées spatiales) par le fait que le neutrino a une masse quasiment nulle (donc un comportement cinématique proche de celui de la lumière dans les laboratoires) et n'interagit que par la force faible.

En chimie, un composé chimique est chiral s'il n'est pas superposable à son image dans un miroir. Si une molécule est chirale, elle possède deux formes énantiomères : une lévogyre (« qui tourne à gauche », du latin laevus : gauche) et une dextrogyre (« qui tourne à droite », du latin dexter : droite) qui font tourner un rayonnement polarisé de manière opposée.

Les organismes vivants possèdent des caractéristiques communes de symétrie et de dissymétrie. Ces deux propriétés ne concernent pas uniquement l'organisation externe de ces organismes mais impliquent aussi tous leurs niveaux d'organisation jusqu'aux molécules qui les constituent. En tant que biosignature, la chiralité est omniprésente dans le monde vivant, depuis l'homochiralité des molécules biologiques jusqu'à la chiralité morphologique. Le passage de l'hétérochiralité à l'homochiralité est un processus qui se déroule en trois étapes : la perte de symétrie, l'enrichissement chiral (enrichissement énantiomérique des acides aminés prébiotiques) et la transmission chirale. La chiralité moléculaire et la chiralité cellulaire se traduisent en une asymétrie multicellulaire (morphogenèse asymétrique) acquise sous l'effet de facteurs déterministes de l'évolution (asymétrie de croissance, contraintes de surface et de volume, nombreux facteurs liés à des structures atomiques ou moléculaires anisotropes) soumis au filtre de la sélection naturelle, et de facteurs stochastiques (hasard de la dérive génétique aléatoire)^[3],[4].

Le type de symétrie d'un organisme est généralement lié à son mode de vie.
Les organismes unicellulaires ou planctoniques possèdent une symétrie sphérique ou circulaire (l'effet de la gravité sur ces êtres de très petite taille est négligeable comparé aux contraintes de tension superficielle, de viscosité du milieu) adaptée à la vie dans des écosystèmes aquatiques continentaux ou marins caractérisés par l'isotropie du milieu physique et des ressources nutritives^[5].
Les animaux sessiles (fixés sur un substrat) ne peuvent pas suivre la piste de leur nourriture ou fuir devant un prédateur, et doivent donc pouvoir couvrir leur environnement à 360°, d'où leur symétrie radiaire. Les animaux plus actifs sont dotés d'une symétrie bilatérale, adaptation liée à des déplacements multidirectionnels (en rapport avec les interactions entre les prédateurs et les proies, la recherche d'un partenaire sexuel ou la migration). Mais cette symétrie bilatérale n'est qu'apparente chez les animaux : chez ceux à déplacement lent, anatomie interne et morphologie externe sont généralement asymétriques alors que chez les ceux à déplacement plus rapide, les asymétries anatomiques fréquentes restent cachées sous une morphologie externe à symétrie presque parfaite. Cette brisure de symétrie est acquise au cours de l'ovogenèse (perte de la symétrie sphérique des gamètes femelles par accumulation de réserves nutritives dans un de leurs pôles), de l'embryogenèse (rôles de la chiralité moléculaire et cellulaire, avec notamment la polarité des cellules qui dépend de nombreux mécanismes moléculaires, comme la répartition asymétrique de certaines protéines cytoplasmiques ou membranaires, ou le réseau de cytosquelette qui présente une asymétrie chirale imposant une chiralité au niveau de la segmentation des blastomères et de la division cellulaire), de l'histogenèse et de l'organogenèse^[6].
À l'inverse des animaux, les plantes ne présentent pas de chiralité morphologique. Chez la majorité d'entre elles, l'embryogenèse est une étape de morphogenèse qui aboutit à la formation d'un axes de symétrie (l'axe radial qui traduit la mise en place des différents tissus) et un d'un axe de polarité (l'axe apico-basal correspondant à la mise en place des différents organes). Cependant, certaines d'entre elles montrent une croissance chirale : l'enroulement hélicoïdal de la vrille (feuille modifiée) ou de la tige volubile des plantes grimpantes en offre un exemple classique. De même, la phyllotaxie ou l'inflorescence des plantes présentent fréquemment dans leur développement une chiralité bien définie^[7].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Chirality (mathematics) » (voir la liste des auteurs).

• Chiralité (chimie)
• Orientation (mathématiques)

• « Chiralité, du neutrino à l'escargot », La Méthode scientifique, France Culture, 3 novembre 2020.
• (histoire des sciences) le pouvoir rotatoire des solutions chirales (Fresnel 1822) analysé sur le site Bibnum.

• Portail de la géométrie
• Portail de la physique
• Portail de la chimie