| Unités SI | newton mètre carré par kilogramme carré (N m2 kg−2) |
|---|---|
| Dimension | M −1·L 3·T −2 |
| Base SI | mètre cube par kilogramme par seconde carrée m3 kg−1 s−2 |
| Nature | Grandeur scalaire |
| Symbole usuel | G |
| Valeur | 6,674 30(15) × 10−11 m3 kg−1 s−2 |
En physique, la constante gravitationnelle, aussi connue comme la constante universelle de gravitation, notée , est la constante de proportionnalité de la loi universelle de la gravitation d'Isaac Newton. Cette constante physique fondamentale apparaît dans des lois de l'astronomie classique qui en découlent (gravité à la surface d'un corps céleste, troisième loi de Kepler[1], etc.), ainsi que dans la théorie de la relativité générale d'Albert Einstein.
Noms
[modifier | modifier le code]La constante est aussi connue comme :
- la constante de Newton[2] en l'honneur[3] d'Isaac Newton (-) car elle intervient dans l'expression de la loi que le savant britannique a proposée en [4] ;
- la constante de Cavendish[2] en l'honneur de[5] Henry Cavendish (-) qui a réalisé, en , une expérience permettant d'estimer la valeur de la constante[6] ;
- le grand G[7],[8] en raison de son symbole usuel G[9] .
Analyse dimensionnelle
[modifier | modifier le code]D'après Newton, la gravitation est une force d'attraction entre deux corps massifs qui, d'une part, est directement proportionnelle au produit de leur masse et, d'autre part, est inversement proportionnelle au carré de la distance qui sépare leur centre de masse respectif :
L'analyse dimensionnelle permet de comparer la dimension d'une force :
et la dimension de :
où est la dimension d'une masse, celle d'une longueur et celle d'un temps.
Les deux termes n'étant pas de même dimension, la relation de proportionnalité permet de définir un facteur de sorte que :
Ce facteur est donc de dimension :
Dans le système international d'unités, il s'exprime donc en m3 kg−1 s−2.
On distingue parfois les masses inertes des masses graves. Les masses reliées aux forces par l'équation fondamentale de la dynamique sont des masses inertes, les masses à l'origine du champ gravitationnel sont des masses graves. En physique classique, la loi de l'action et de la réaction implique que la force d'attraction est symétrique entre deux corps de masses respectives et , et donc que masse grave et masse inerte sont identiques. En mécanique relativiste, l'identité entre masse inerte et masse grave fait l'objet du principe d'équivalence. Il est cependant possible d'imaginer une mécanique newtonienne dans laquelle ces deux masses seraient différentes pour une substance donnée (mais de même dimension).
Notation
[modifier | modifier le code]C'est en que les physiciens français Alfred Cornu (-) et Jean-Baptistin Baille (-) introduisent explicitement une constante qu'ils nomment « constante de l'attraction » et notent [10],[3],[11].
La constante est couramment notée , symbole correspondant à la lettre G majuscule de l'alphabet latin en italique.
D'après John J. Roche[12] et John D. Barrow[13], ce symbole a été introduit, en 1885, par Arthur König et Franz Richarz[14].
Valeur
[modifier | modifier le code]La constante gravitationnelle est une constante de proportionnalité de la force de gravitation (c'est-à-dire d'attraction entre les corps), cette dernière suivant la loi en carré inverse des distances et étant proportionnelle au produit des masses et .
Valeur dans le Système international
[modifier | modifier le code]correspond à la force entre deux masses d'un kilogramme chacune, distantes d'un mètre.
En 2018, le CODATA recommande la valeur suivante[15], en unités SI :
où le nombre entre parenthèses est l'incertitude standard sur les derniers chiffres explicités, c'est-à-dire :
- ,
soit une incertitude relative de :
- , soit à 22 ppm près.
L'unité dérivée m3 kg−1 s−2 peut aussi être écrite N m2 kg−2.
Valeur dans le système CGS
[modifier | modifier le code]Dans le système CGS la valeur de la constante est :
- .
Valeur en unités naturelles
[modifier | modifier le code]Dans les unités dites « naturelles », et les autres constantes physiques comme la vitesse de la lumière ont pour valeur 1.
Nouvelles valeurs obtenues
[modifier | modifier le code]D'après le rapport d'Erland Myles Standish (en) à l'Union astronomique internationale, en 1994, la meilleure estimation de la valeur de G était :
En 2007, J. B. Fixler, G. T. Foster, J. M. McGuirk et M. A. Kasevich ont obtenu la valeur suivante[16] :
Dans une étude menée en 2010, Harold V. Parks et James E. Faller[17] ont obtenu une valeur différente de celle déjà trouvée :
En 2014 le CODATA recommandait la valeur suivante (supplantée maintenant par la valeur CODATA 2018)[15], en unités SI :
soit une incertitude relative de .
Comparaison avec les autres forces fondamentales
[modifier | modifier le code]
Quand on compare les quatre forces fondamentales (force de gravitation, force électromagnétique, force faible, force forte), il apparaît que la force de gravitation est de très loin la plus faible de toutes. Par exemple, la force de gravitation entre un électron et un proton séparés par un mètre vaudrait environ 10-67 newton, tandis que la force électromagnétique entre les deux mêmes particules à la même distance vaudrait environ 10-28 newton, c'est-à-dire 39 ordres de grandeur (ou 1039 fois) plus importante.
Mesures de la constante gravitationnelle
[modifier | modifier le code]La constante gravitationnelle est l'une des constantes les plus difficiles à mesurer.
a été mesurée directement la première fois par Henry Cavendish[18] en 1798, inspiré par l'œuvre de John Michell. Il utilisa une balance de torsion avec deux boules en plomb placées le long d'une tige horizontale. La connaissance du moment d'inertie de l'ensemble tige+boules et de la constante de torsion du fil de suspension permet de calculer la fréquence des oscillations de la balance. La très faible attraction causée par deux autres boules, placées indépendamment à l'extrémité de la tige, cause une légère modification des oscillations, et permet de calculer la force de gravité entre les boules, et ainsi la valeur de la constante de gravitation. Cavendish trouve . Cependant, son but n'était pas de mesurer cette constante, mais de mesurer la masse de la Terre.
La précision de la valeur mesurée de a peu changé depuis cette première expérience. Cela est dû, non seulement à la faiblesse de la force de gravitation, mais aussi à l'impossibilité de s'affranchir réellement de la présence d'autres objets massifs (comme les murs du laboratoire...). Une très légère vibration du sol (provoquée par exemple par le passage d'un camion dans la rue) peut aussi compromettre la précision de la mesure. Une récente étude (Gillies, 1997) a montré que les valeurs publiées de la constante varient beaucoup, et que des mesures plus récentes et plus précises s'excluent mutuellement.
Historiquement, l’existence de cette constante apparaît donc avec la loi de la gravitation de Newton mais ne pouvait constituer à ce stade qu’une hypothèse.
La détermination de sa valeur a été réalisée à partir des expériences de Cavendish (1798). Les résultats de cette époque convergeaient vers une valeur unique (à des erreurs expérimentales acceptables près) démontrant par la même occasion l’existence de la constante.
Constantes associées
[modifier | modifier le code]Paramètre gravitationnel standard
[modifier | modifier le code]Le produit s'appelle le paramètre gravitationnel standard, noté (mu).
Ce paramètre fournit une simplification pratique des différentes formules liées à la gravitation.
Selon que désigne la masse de la Terre ou du Soleil, s'appelle la constante gravitationnelle géocentrique ou héliocentrique.
En fait, pour la Terre et le Soleil, ce produit est connu avec une plus grande précision que celle associée à chacun des deux facteurs et . Il est ainsi possible d'utiliser la valeur du produit connue avec une plus grande précision, plutôt que de substituer les valeurs des deux paramètres.
- Pour la Terre : , soit à 0,002 ppm = 2 ppb près, ce qui est 10 000 fois mieux que G seule.
- Pour le Soleil : , soit à 0,06 ppb près, ce qui est 366 666 fois mieux que G seule.
Constante gravitationnelle de Gauss
[modifier | modifier le code]De même, les calculs de la mécanique céleste peuvent être faits dans les unités de masse solaire plutôt que celles du Système international d'unités, comme le kilogramme.
Dans ce cas, on utilise la constante gravitationnelle de Gauss[19], qui se note :
avec :
- est une unité astronomique ;
- est le jour solaire moyen ;
- est la masse solaire.
Si à la place du jour solaire moyen, on utilise l'année sidérale comme unité de temps, la valeur de est alors très proche de .
Voir aussi
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- George T. Gillies. « The Newtonian gravitational constant: recent measurements and related studies ». Reports on Progress in Physics ; 60 : 151-225, 1997. (A lengthy, detailed review. See figure 1 and table 2 in particular. Disponible en ligne : PDF.)
- (en) Erland Myles Standish, « Report of the IAU WGAS Sub-group on Numerical Standards », dans Immo Appenzeller (éd.), Highlights of Astronomy, vol. 10, Dordrecht, Kluwer Academic Publishers, . (Rapport complet disponible en ligne : PostScript. Tableaux du rapport aussi disponibles : Astrodynamic Constants and Parameters.)
- Jens H. Gundlach et Stephen M. Merkowitz. « Measurement of Newton's Constant Using a Torsion Balance with Angular Acceleration Feedback ». Physical Review Letters, 85(14):2869-2872, 2000. (Aussi disponible en ligne : PDF.)
- Peter J. Mohr et Barry N. Taylor, CODATA recommended values of the fundamental physical constants: 2002 (Reviews of Modern Physics, 2005, vol. 77, p. 1–107). PDF, section Q (p. 42–47) décrit les expériences de mesures mutuellement exclusives à partir desquelles la valeur CODATA de G est dérivée.
- [Parsons et Dixon 2017] Paul Parsons et Gail Dixon (trad. de l'anglais par Charles Frankel), 50 clés pour comprendre les grandes idées de la science [« 50 ideas you really need to know science »], Malakoff, Dunod, coll. « 50 clés pour comprendre », , 1re éd., 1 vol., 207, ill., 17 × 20 cm (ISBN 978-2-10-076039-8, EAN 9782100760398, OCLC 974995722, BNF 45218772, SUDOC 199281548, présentation en ligne, lire en ligne).

- [Pecker 2003] Jean-Claude Pecker, L'Univers exploré, peu à peu expliqué, Paris, O. Jacob, coll. « Sciences », , 1re éd., 1 vol., 335, ill., 15,5 × 24 cm (ISBN 2-7381-1188-2, EAN 9782738111883, OCLC 402244445, BNF 39002977, SUDOC 07139088X, présentation en ligne, lire en ligne).

- [Semay et Silvestre-Brac 2016] Claude Semay et Bernard Silvestre-Brac, Relativité restreinte : bases et applications, Paris, Dunod, coll. « Sciences sup », , 3e éd. (1re éd. ), 1 vol., X-309, ill., 17 × 24 cm (ISBN 978-2-10-074703-0, EAN 9782100747030, OCLC 945975983, BNF 45019762, SUDOC 192365681, présentation en ligne, lire en ligne).

- [Uzan et Lehoucq 2005] Jean-Philippe Uzan et Roland Lehoucq, Les constantes fondamentales, Paris, Belin, coll. « Belin Sup / Histoire des sciences / Physique », , 1re éd., 1 vol., 487, ill., 17 × 24 cm (ISBN 978-2-7011-3626-4, EAN 9782701136264, OCLC 300532710, BNF 39295528, SUDOC 087569523, présentation en ligne), 3e part. (« La constante de gravitation G »). — La section sur la constante de gravitation contient, entre autres, une traduction française des articles originaux de Maskeline, Cavendish sur la mesure de la constante de gravitation et une traduction des textes de Dirac, Gamow et Teller sur l'hypothèse d'une constante de gravitation variable.
- [Taillet, Villain et Febvre 2018] Richard Taillet, Loïc Villain et Pascal Febvre, Dictionnaire de physique, Louvain-la-Neuve, De Boeck Supérieur, hors coll., , 4e éd. (1re éd. ), 1 vol., X-956, ill., fig. et graph., 17 × 24 cm (ISBN 978-2-8073-0744-5, EAN 9782807307445, OCLC 1022951339, BNF 45646901, SUDOC 224228161, présentation en ligne, lire en ligne).
 .
.
Articles connexes
[modifier | modifier le code]- Constante d'Einstein
- Henry Cavendish
- Hypothèse des grands nombres de Dirac
- Seconde (temps)
- Table des constantes astrophysiques
- Unités de Planck
Liens externes
[modifier | modifier le code]- (en) The International System of Units (SI) (site du Bureau International des Poids et Mesures).
- (en) Valeurs CODATA (Committee on Data for Science and Technology) internationalement recommandées des constantes fondamentales de la physique.
- (en) Débat à propos des méthodes de mesure de la constante gravitationnelle.
- (fr) Illustration du pendule de Cavendish ou : comment mesurer les masses de l'Univers.
- (fr) Description d'un rapport de travail pratique Université de Neuchâtel.
- (en) G-whizzes disagree over gravity (dispersion des résultats de mesure), Nature, 23 août 2010.
- (en) Simple pendulum determination of the gravitational constant.
Notes et références
[modifier | modifier le code]- Dans sa forme initiale la troisième loi de Kepler indique seulement qu'une certaine expression est constante. Après l'énoncé de la loi de la gravitation il est apparu que cette constante est directement liée à G.
- Semay et Silvestre-Brac 2016, p. 112, n. 10.
- Taillet, Villain et Febvre 2018, s.v.gravitation (constante de la), p. 346, col. 1.
- Taillet, Villain et Febvre 2018, s.v.force gravitationnelle, p. 314, col. 1.
- Pecker 2003, p. 175-176 et p. 235.
- Taillet, Villain et Febvre 2018, s.v.Cavendish (expérience de) [sens 1], p. 104, col. 2.
- Parsons et Dixon 2017, p. 15.
- Rupert Sheldrake, Réenchanter la science, Paris, Albin Michel, , 432 p. (ISBN 978-2-226-28910-0, lire en ligne), en ligne sur Google Livres (consulté le 11 juillet 2014).
- Taillet, Villain et Febvre 2018, s.v.G [sens 1], p. 328, col. 1.
- (en) Clive Speake et Terry Quinn, « The search for Newton's constant », Physics Today, vol. 67, no 7, , p. 27-33 (DOI 10.1063/PT.3.2447, Bibcode 2014PhT....67g..27S, lire en ligne [PDF]) — p. 28, col. 2.
- A. Cornu et J. Baille, « Détermination nouvelle de la constante de l'attraction et de la densité moyenne de la Terre », Comptes rendus hebdomadaires des séances de l'Académie des sciences, t. LXXVI, no 15, , p. 954-958 (lire en ligne) — p. 954.
- (en) John J. Roche, The Mathematics of Measurement : A Critical History, Londres, Athlone Press, , X-330 p. (ISBN 0-387-91581-8, OCLC 40499222), p. 161 (lire en ligne [html])
- John D. Barrow (trad. de l'anglais), Les Constantes de la nature, Paris, Odile Jacob, , 332 p. (ISBN 2-7381-1671-X, OCLC 63682144, BNF 40047556, lire en ligne), p. 291, n. 43 (lire en ligne [html])
- (de) Arthur König et Franz Richarz, « Eine neue Methode zur Bestimmung der Gravitationsconstante », Annalen der Physik und Chemie, vol. 260, no 4, , p. 664-668 (DOI 10.1002/andp.18852600409, Bibcode 1885AnP...260..664K, lire en ligne [PDF], consulté le ).
- (en) « CODATA 2018 Newtonian constant of gravitation », NIST, (consulté le ).
- (en) J. B. Fixler, G. T. Foster, J. M. McGuirk et M. A. Kasevich, « Atom Interferometer Measurement of the Newtonian Constant of Gravity », Science, vol. 315, no 5808, , p. 74-77 (DOI 10.1126/science.1135459, Bibcode 2007Sci...315...74F)
- (en) Harold V. Parks et James E. Faller, « A Simple Pendulum Determination of the Gravitational Constant », Physical Review Letters, vol. 105, no 11, , p. 110801-110805 (DOI 10.1103/PhysRevLett.105.110801, arXiv 1008.3203v3, lire en ligne [PDF], consulté le )
- (en) Experiments to Determine the Density of the Earth, Philosophical Transactions of the Royal Society of London, 1798
- (en) Dictionary of Technical Terms for Aerospace Use - G.









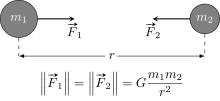
![{\displaystyle [G]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3653325703ef26276d0dba085839c2e8635db680)


![{\displaystyle [|\mathbf {F} |]=M\cdot L\cdot T^{-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fdca361948e24ce00c4523516e3a4038953854d)

![{\displaystyle \left[{\frac {{m_{1}}{m_{2}}}{r^{2}}}\right]=M^{2}\cdot L^{-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/996e8ca78aaea13a3c39b701f1b2a9644f9cc0ef)




![{\displaystyle [G]={\frac {[|\mathbf {F} |][r^{2}]}{[{m_{1}}{m_{2}}]}}=M^{-1}\cdot L^{3}\cdot T^{-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd7bc36d7dd57f9ff2523831084faf6b26be7b8f)



























