En mathématiques, et en particulier dans l'étude des systèmes dynamiques, un diagramme de bifurcation illustre les valeurs visitées asymptotiquement (points fixes, points périodiques, attracteurs chaotiques) par un système en fonction d'un paramètre[1],[2].
Exemples
-
Diagramme de bifurcation pour l'attracteur de Rössler.
-
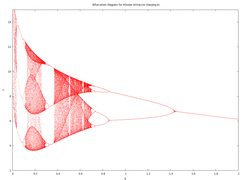
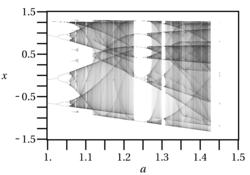
Diagramme de bifurcation pour l'attracteur de Hénon.
-
Diagramme de bifurcation de la fonction tente (en).
-
Diagramme de bifurcation de la fonction de Gauss itérée (en).
Notes et références
- ↑ (en) Tianshou Zhou, « Bifurcation », dans Encyclopedia of Systems Biology, Springer, (ISBN 978-1-4419-9863-7, DOI 10.1007/978-1-4419-9863-7_500, lire en ligne), p. 79–86
- ↑ (en) Christos Volos, Ioannis Kyprianidis, Ioannis Stouboulos et Sundarapandian Vaidyanathan, chap. 7 « Random Bit Generator Based on Non-Autonomous Chaotic Systems », dans Ahmad Taher Azar, Sundarapandian Vaidyanathan, Handbook of Research on Advanced Intelligent Control Engineering and Automation, IGI Global, , 794 p. (ISBN 9781466672482, DOI 10.4018/978-1-4666-7248-2.ch007, lire en ligne), p. 203-229