Cet article ne cite pas suffisamment ses sources ().
Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».
En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?
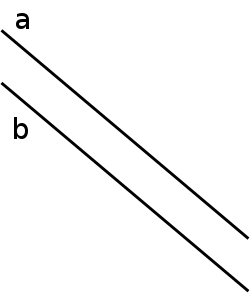
En géométrie affine, deux droites sont dites parallèles si elles ont la même direction, c’est-à-dire si elles ont des vecteurs directeurs colinéaires. Toute droite étant parallèle à elle-même, lorsqu'on veut préciser que deux droites parallèles sont distinctes, on dit qu'elles sont strictement parallèles[1].
Dans un plan affine
Deux droites du plan affine sont parallèles si et seulement si elles n'ont aucun point commun ou si elles sont confondues. Deux droites ayant un et un seul point commun sont dites sécantes.
- Propriétés utiles
- Axiome de Playfair (reformulation du cinquième postulat d'Euclide) : Par un point A n'appartenant pas à une droite D, on ne peut faire passer qu'une droite parallèle à D.
- Soit deux droites parallèles D et D', toute droite sécante à D est sécante à D'.
- Soit deux droites parallèles D et D', toute droite perpendiculaire à D est perpendiculaire à D'.
- Soit deux droites parallèles D et D', toute droite parallèle à D est parallèle à D'.
Le complété projectif d'un espace affine est l'espace affine auquel on rajoute des points à l'infini, un point à l'infini par direction de droites. Une droite affine est complétée en une droite projective en lui rajoutant le point à l'infini correspondant à sa direction.
Deux droites projectives obtenues par complétion de deux droites affines parallèles distinctes ont un point d'intersection unique ; c'est le point à l'infini de chacune des deux droites projectives.
Notes et références
- ↑ « Droites parallèles et perpendiculaires - Cours maths 6ème - Tout savoir sur les droites parallèles et perpendiculaires », sur www.educastream.com (consulté le )
Liens externes
