|
| Diagramme de Venn de |

|
| Diagramme de Venn de |
La fonction OU exclusif, souvent appelée XOR (eXclusive OR) ou disjonction exclusive, ou somme binaire en cryptographie où il est noté +, ou encore ⊻ en algèbre relationnelle, est un opérateur logique de l'algèbre de Boole à deux opérandes, qui peuvent avoir chacun la valeur VRAI ou FAUX. Il associe un résultat qui a lui-même la valeur VRAI seulement si les deux opérandes ont des valeurs distinctes.
Cet opérateur est très utilisé en électronique, en informatique, et aussi en cryptographie du fait de ses propriétés intéressantes.
Son symbole est traditionnellement un signe plus dans un cercle : « ⊕ ».
Définition
Appelons A et B les deux opérandes considérés. Convenons de représenter leur valeur ainsi :
- 1 = VRAI
- 0 = FAUX
L'opérateur XOR est défini par sa table de vérité, qui indique pour toutes les valeurs possibles de A et B la valeur du résultat R :
| Table de vérité de XOR | ||
| A | B | R = A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Comme on peut le voir, l'opérateur logique XOR, ou OU exclusif, peut se définir par la phrase suivante :
- Le résultat est VRAI si un et un seul des opérandes A et B est VRAI
ou
- Le résultat est VRAI si les deux opérandes A et B ont des valeurs distinctes
ou
- Le résultat est VRAI si un nombre impair d'entrées est vrai (ceci est surtout applicable lorsque deux ou plusieurs opérateurs logiques XOR se cascadent (générateurs de bit de parité)
Il se différencie de l'opérateur OU inclusif, car il donne un résultat FAUX lorsque A et B ont simultanément la valeur VRAI. Son symbole se différencie aussi de l'opérateur OU inclusif dont le symbole est simplement un « PLUS » : « + ».
En informatique, cet opérateur peut s'utiliser pour combiner deux bits, valant chacun 0 ou 1, en appliquant les règles définies par la table précédente, le résultat étant lui-même la valeur d'un bit.
Avec des portes logiques ET/OU, A XOR B = (A ET non B) OU (non A ET B).
La fonction XOR est un exemple de fonction parité.
Équivalence, introduction et élimination
La disjonction exclusive , ou Jpq, peut être exprimée en termes de conjonction (« et logique », ), disjonction (« ou logique », ), et de la négation logique () comme suit :
La disjonction exclusive peut aussi être formulée de la façon suivante :
Cette représentation de XOR peut être utile lors de la construction d'un circuit ou d'un réseau, car il n'a qu'une seule opération et un nombre réduit d'opérations et . Une preuve de cette identité est donnée ci-dessous:
- Il est parfois utile de noter de la manière suivante:
ou:
Cette équivalence peut être établie en appliquant les lois de De Morgan deux fois à la quatrième ligne de la démonstration ci-dessus.
Le ou exclusif est également équivalent à la négation d'une équivalence logique, par les règles de l'implication matérielle.
En résumé, nous avons :
Quelques propriétés mathématiques
- (on le vérifie facilement sur la table pour les 2 valeurs possibles de A)
- Commutativité
- Associativité
- et où est la fonction coïncidence.
- si et seulement si (dans un sens, c'est immédiat, dans l'autre, utilisation de la propriété d'associativité et de la propriété : )
- On déduit de cette propriété : ou même encore : et même encore :
- alors et
- (Conséquence des deux premières propriétés et de l'associativité — utile en cryptographie (voir ci-dessous))
- L'ensemble {0;1} muni des deux lois de composition interne OU exclusif et ET est un corps fini.
Exemple d'utilisation en cryptographie
Considérons un document numérique à chiffrer, il consiste en une suite de bits. Dans la méthode de chiffrement par flot, on doit disposer par ailleurs d'une suite de bits de même longueur, totalement aléatoire, que l'on appelle clé de chiffrement. On traite un à un les bits du document en clair, en le combinant avec le bit de même rang de la clé de chiffrement.
Appelons A un bit en clair et B le bit de même rang de la suite aléatoire.
Le chiffrement consiste à calculer le bit C par : C = A ⊕ B . C est le chiffré de A.
Pour déchiffrer C on utilise à nouveau le bit B de la suite aléatoire et on calcule : C ⊕ B.
Le résultat donne A, le bit en clair, car C ⊕ B = A ⊕ B ⊕ B = A ⊕ 0 = A, en utilisant les deux premières propriétés ci-dessus.
Cette méthode est l'une des manières d'effectuer un chiffrement symétrique, où la même clé sert à chiffrer et déchiffrer.
Ce système, bien que très simple dans son principe, peut s'avérer inviolable si la suite de bits de la clé est vraiment aléatoire. Cette dernière ne doit en outre être utilisée qu'une seule fois (on parle de masque jetable, ou encore de « one-time pad »). Dans cette phrase, c'est surtout le mot « aléatoire » qui s'avère être le plus difficile à mettre en œuvre. Mais lorsque la clé est vraiment aléatoire (techniquement, qu'elle est tirée selon la distribution uniforme parmi toutes les suites possibles de cette longueur), ce système est parfaitement sûr, en un sens rigoureusement défini par Claude Shannon, en 1949, dans un article fondateur « Communications theory of secrecy systems ». Il convient d'ajouter que c'est le seul chiffrement aboutissant à une sécurité absolue, en théorie.
Voir aussi l'article : masque jetable
Illustration
Voici un exemple numérique de la méthode précédente :
M = 0110101011010100 (message en clair)
K = 0101011011100110 (la clé ; à garder secrète bien évidemment)
Convenons que le symbole ⊕ représente ici l'application de l'opérateur XOR à chacun des bits
Pour chiffrer, il faut utiliser la table de vérité: « M » est votre message et « K » représente la clé secrète.
Donc: M ⊕ K = C. Le « C » représente le message chiffré:
Chiffrement : C = M ⊕ K = 0011110000110010 (message chiffré)
Déchiffrement : M = C ⊕ K = 0110101011010100 (message déchiffré)
Histoire
Ce système de chiffrement a été utilisé pour le téléphone rouge, en fait un télex, reliant directement le Kremlin à la Maison-Blanche, les clés transitant alors par valises diplomatiques. Le système de masque jetable était également employé par les espions soviétiques. Certains masques furent utilisés plus d'une fois (parfois avec des années d'intervalle) ce qui permit aux services du chiffre anglais de déchiffrer certains messages.
Autres applications en cryptographie
La totalité des chiffreurs symétriques utilise l'opérateur XOR. L'algorithme de cryptographie haute sécurité symétrique AES (Rijndael) en particulier, en utilise un très grand nombre.
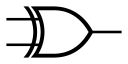
Application en électronique
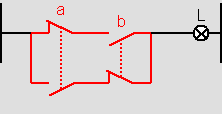
Exemple d'utilisation : le circuit intégré 7486 TTL ou le circuit intégré CMOS 4070 intègre quatre portes logiques du type OU exclusif. Illustration : Exemple : La lampe s'allume si l'on appuie sur « a » ou « b » seulement, mais pas si l'on appuie sur « a » et « b » simultanément.
- Équation
Applications en informatique
Outre les utilisations liées à la cryptographie, la fonction OU exclusif permet de remettre rapidement la valeur d'une variable (souvent un registre) à zéro.
Prenons par exemple le code en assembleur qui utilise le OU exclusif pour remettre la valeur du registre eax à zéro :
xor eax, eax
Sur les processeurs de type x86, cette instruction est plus courte (en nombre d'octets) que le code intuitif suivant :
mov eax, 0
Elle permet aussi la mise à zéro d'une variable lorsque les conditions ne permettent pas l'octet 0x00 dans le binaire (shellcode).
On peut également utiliser le OU exclusif pour échanger deux variables sans utiliser de variable temporaire.
Application en électricité domestique
Une application utilisée de l'opérateur logique OU exclusif en électricité domestique est dans les salles où une ampoule peut être allumée ou éteinte par deux interrupteurs placés près de deux entrées. Chacun des deux interrupteurs peut soit allumer ou éteindre l'ampoule quelle que soit la position de l'autre interrupteur. Pour obtenir une telle fonctionnalité, on doit brancher les deux interrupteurs afin de former un opérateur XOR. C'est le montage dit « va-et-vient ».
Notes et références
Voir aussi
Articles connexes
- Fonction logique
- Fonction OUI
- Fonction NON
- Fonction ET
- Fonction OU
- Fonction NON-ET
- Fonction NON-OU
- Fonction Coïncidence
Liens externes
- Notices dans des dictionnaires ou encyclopédies généralistes :











![{\displaystyle {\begin{matrix}p\oplus q&=&(p\land \lnot q)&\lor &(\lnot p\land q)\\[3pt]&=&((p\land \lnot q)\lor \lnot p)&\land &((p\land \lnot q)\lor q)\\[3pt]&=&((p\lor \lnot p)\land (\lnot q\lor \lnot p))&\land &((p\lor q)\land (\lnot q\lor q))\\[3pt]&=&(\lnot p\lor \lnot q)&\land &(p\lor q)\\[3pt]&=&\lnot (p\land q)&\land &(p\lor q)\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9d13922496dd48e20bbace8ae95ee59f340df07)


![{\displaystyle {\begin{matrix}p\oplus q&=&(p\land \lnot q)&\lor &(\lnot p\land q)&=&p{\overline {q}}+{\overline {p}}q\\[3pt]&=&(p\lor q)&\land &(\lnot p\lor \lnot q)&=&(p+q)({\overline {p}}+{\overline {q}})\\[3pt]&=&(p\lor q)&\land &\lnot (p\land q)&=&(p+q)({\overline {pq}})\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aede2a23b5b43fb562e687bf13cf4e9156ba8e8)