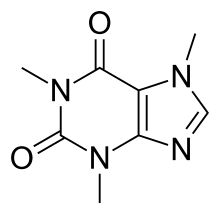
En théorie des graphes chimiques et en chimie mathématique, un graphe moléculaire ou chimique est une représentation de la formule développée d'un composé chimique en termes de théorie des graphes. Un graphe moléculaire est un graphe étiqueté dont les sommets correspondent aux atomes du composé et les arêtes correspondent aux liaisons chimiques. Ses sommets sont étiquetés avec les types d'atomes correspondants et les arêtes sont étiquetés avec les types de liaisons^[1]. Pour des raisons particulières, n'importe quelle étiquette peut être ignorée.

Il existe des graphes moléculaires dans lesquels les sommets correspondant à l'hydrogène sont éliminés.

Les graphes moléculaires peuvent faire la distinction entre les isomères structuraux (tels que l'isopentane et le néopentane) qui possèdent la même formule moléculaire mais des graphes non isomorphes. En revanche, le graphe moléculaire ne contient normalement aucune information sur la disposition tridimensionnelle des liaisons et ne peut donc pas distinguer les isomères cis-trans (tels que les 2-butène cis et trans) et les stéréoisomères (tels que les D- et L- glycéraldéhyde).

Dans certains cas importants (calcul d’indice topologique, etc.), la définition classique suivante est suffisante : le graphe moléculaire est un graphe connecté non orienté correspondant à la formule développée du composé chimique de sorte que les sommets du graphe correspondent aux atomes de la molécule et que les arêtes du graphe correspondent aux liaisons chimiques entre ces atomes^[2]. Une variante consiste à représenter les matières sous forme de graphes euclidiens infinis, en particulier les cristaux sous forme de graphes périodiques^[3].

Arthur Cayley fut probablement le premier à publier des résultats concernant les graphes moléculaires dès 1874, avant même l’introduction du terme " graphe "^[4]. Pour dénombrer des isomères, Cayley a considéré des "diagrammes" constitués de points marqués par des atomes et reliés par des liens dans un assemblage. Il a ensuite introduit les termes plérogramme et kénogramme qui sont respectivement le graphe moléculaire et le graphe moléculaire avec suppression d'hydrogène^[5]. Si l'on continue à supprimer davantage les atomes reliés par un seul lien, on arrive à un simple kénogramme, éventuellement vide^[6].

Danail Bonchev, dans sa Chemical Graph Theory (théorie des graphes chimiques), retrace les origines de la représentation des forces chimiques par des diagrammes que l'on pourrait appeler "graphes chimiques" dès le milieu du XVIIIe siècle. Au début du XVIIIe siècle, la notion de gravité d'Isaac Newton avait conduit à des idées spéculatives voulant que les atomes soient maintenus ensemble par une sorte de "force gravitationnelle". En particulier, depuis 1758, le chimiste écossais William Cullen dans ses conférences, utilisait ce qu'il appelait des "diagrammes d'affinité" pour représenter des forces supposées exister entre des paires de molécules dans une réaction chimique. Dans un livre de William Higgins datant de 1789, des diagrammes similaires ont été utilisés pour représenter les forces au sein de molécules. Ces diagrammes et certains autres contemporains n’avaient aucun lien avec les liaisons chimiques : cette dernière notion n’a été introduite qu’au siècle suivant^[7].

• Portail de la chimie