Pour les articles homonymes, voir Stoner.

Le modèle de Stoner-Wohlfarth est le modèle le plus simple permettant d’expliquer la physique des grains magnétiques monodomaines (composés d'un seul domaine magnétique)^[1],[2]. Il permet le calcul du cycle d’hystérésis de la particule et se révèle très efficace dans le cas de petites particules magnétiques avec une forte anisotropie. Il est donc essentiel pour la description des systèmes de stockage de données ferromagnétiques, en biomagnétisme, magnétisme des roches ou encore en paléomagnétisme.

En 1946, Erich Peter Wohlfarth (en) obtient sa licence en physique à l’Université de Leeds^[3]. Il continue son doctorat à cette même université sous la direction du Professeur Edmund Clifton Stoner (en).  Il obtient son doctorat en 1948. En cette même année ils publient ensemble l’article “A mechanism of magnetic hysteresis in heterogeneous alloys”^[1]. Le modèle dans cet article est connu aujourd'hui comme le modèle Stoner-Wohlfarth. Celui-ci a aidé à comprendre le comportement des matériaux ferromagnétiques tels que le fer et les changements de propriétés magnétiques avec la température. Il a ensuite été appliqué pour le développement des mémoires magnétiques modernes.

Ces travaux furent ensuite repris par John P. Slonczewski dans une recherche IBM non publiée, qui traça le résultat du modèle sous la forme d’une astroïde.

Ce modèle nécessitant le calcul de l’intégrale d’une multitude de pôles d’aimantation orientées aléatoirement, il se fait aujourd’hui facilement par ordinateur, toutefois, au moment de son élaboration, M. Stoner et M.Wohlfarth le faisaient à la main et par calcul trigonométriques.

Dans le modèle de Stoner-Wohlfarth, l'aimantation est représentée par le vecteur ${\displaystyle M}$. Ce vecteur peut tourner lorsque le vecteur ${\displaystyle H}$ (le champ magnétique) change. On considère ensuite l’axe magnétique d’anisotropie de paramètre ${\displaystyle K_{u}}$. Cet axe représente l’axe facile d'aimantation, qui est favorable énergétiquement. Selon cet axe, les deux directions sont généralement équivalentes. Lorsque le champ ${\displaystyle H}$ augmente, l’aimantation ${\displaystyle M}$ tend à s’aligner le long de celui-ci. Un équilibre s’établit dans une direction entre l’axe de facile aimantation et la direction du champ magnétique pour de faibles champs. Sous forts champs, l’aimantation ${\displaystyle M}$ est complètement alignée avec ${\displaystyle H}$.

Lors d’une variation du champ ${\displaystyle H}$, l’aimantation reste dans le plan défini par le vecteur ${\displaystyle H}$, et l’axe de facile aimantation. Nous considérons les angles ${\textstyle \varphi }$ entre ${\displaystyle M}$ et ${\textstyle H}$ et ${\textstyle \theta }$ entre ${\textstyle H}$ et l’axe de facile aimantation.

L’énergie du système est constituée de deux sous-énergies : La première (${\displaystyle E_{a}}$) est due à l’axe d’anisotropie (autre nom de l’axe de facile aimantation), pondérée par le coefficient ${\displaystyle K_{u}}$. La seconde (${\displaystyle E_{z}}$) est l’énergie Zeeman liée à la valeur du champ ${\displaystyle H}$.

${\displaystyle E_{a}=K_{u}\sin ^{2}(\varphi -\theta )}$

${\displaystyle E_{z}=-\mu _{0}{\vec {M}}\cdot {\vec {H}}=-\mu _{0}HM_{s}\cos(\varphi )}$

L'énergie du système est

${\displaystyle E=V(E_{a}+E_{z})=K_{u}V\sin ^{2}(\varphi -\theta )-\mu _{0}M_{s}VH\cos(\varphi )}$ (1)

où ${\displaystyle V}$ est le volume de l'échantillon, ${\displaystyle M_{s}}$ est la valeur de l'aimantation à saturation et ${\displaystyle \mu _{0}}$ est la permittivité du vide.

Un système tend toujours à minimiser son énergie, nous cherchons donc les minimums de cette formule pour des orientations de l’axe d'anisotropie et de ${\displaystyle H}$. Nous pouvons comparer cette réflexion à un objet soumis à la force de gravitation. Plus l’objet est haut, plus son énergie potentielle de pesanteur est grande. Si une balle est lâchée, elle va tomber, puis rouler jusqu’au point le plus bas, dans un creux. Ce faisant, elle diminue son énergie potentielle. Pour notre système, il n’y a pas de déplacement, mais un angle d’aimantation, et celui-ci peut varier afin de minimiser l’énergie du système.

E.C. Stoner et E.P. Wohlfarth ont normalisé l'équation, avec ${\displaystyle h={\mu _{0}M_{s}H \over 2K_{u}}}$:

${\displaystyle \eta ={E \over 2K_{u}V}={1 \over 4}-{1 \over 4}\cos(2(\varphi -\theta ))-h\cos(\varphi )}$ (2)

Cette équation est représentée sur la figure 2 pour un angle de facile aimantation donné. On voit bien que le minimum varie en fonction de l'axe de la direction d'aimantation. Pour ${\displaystyle h=0}$, ce qui correspond à ${\displaystyle H=0}$, il y a deux positions stables; 15° et 195° sur le graphique.

Pour trouver les extremums, il faut dériver ${\displaystyle \eta }$ :

${\displaystyle {\partial \eta \over \partial \varphi }={1 \over 2}\sin(2(\varphi -\theta ))+h\sin(\varphi )=0}$ (3)

Ensuite, il faut différencier les maximums des minimums; la dérivée seconde doit être positive car nous cherchons des minima:

${\displaystyle {\partial ^{2}\eta \over \partial \varphi ^{2}}=\cos(2(\varphi -\theta ))+h\cos(\varphi )>0}$ (4)

En général, le champ ${\displaystyle H}$ varie selon un seul axe, passant d’une valeur positive à une valeur négative. Pour toute valeur de ${\displaystyle H}$, nous pouvons déterminer une valeur de ${\displaystyle \varphi }$. Nous posons enfin : ${\displaystyle m_{h}=\cos(\varphi )}$

Cela permet de tracer ${\displaystyle m_{h}}$ en fonction de ${\displaystyle h}$. Deux solutions apparaissent pour l'équation 3 pour chaque valeur de ${\displaystyle \varphi }$ soit deux ou quatre valeurs suivant ${\displaystyle h}$. Cependant, sur une partie de ces courbes, l’équation 4 n’est pas respectée. Il y a donc un seul état stable pour les valeurs élevées de ${\displaystyle H}$, avec ${\displaystyle M}$ presque aligné avec ${\displaystyle H}$. Pour de faibles valeurs de ${\displaystyle H}$, deux valeurs sont possibles.

Lorsque l’on sort de ce domaine, cela conduit à passer au seul état d’équilibre, et donc à sauter d’une courbe à l’autre. Sur le graphique ${\displaystyle \eta (\varphi )}$ (Figure 2), cela revient au passage d’un minimum à un maximum, l'aimantation « tombe » dans ce qui était le deuxième minimum, et est devenu le seul minimum. Lors d’une montée ou une descente de ${\displaystyle H}$ (qui est proportionnel à ${\displaystyle h}$), la figure n’est donc pas la même : nous parlons de cycle d’hystérésis. Prenons en exemple le graphique ci-contre en partant de ${\displaystyle h=-2}$, en effectuant une montée jusqu’à ${\displaystyle h=2}$, puis une redescente. Sur le graphique, nous partons d’en bas à gauche, nous nous déplaçons horizontalement vers la droite : le champ augmente, mais la direction d’aimantation ne varie presque pas (${\displaystyle m_{h}\approx -1}$, ${\displaystyle \varphi \approx 0}$). Ensuite nous nous approchons du point d’inflexion où ${\displaystyle h=0{,}6}$, ${\displaystyle m_{h}=-0{,}64}$ et ${\displaystyle \varphi =47^{\circ }}$. La double dérivée passe négative, nous ne sommes plus sur un minimum d’énergie : nous sautons sur la courbe bleue à ${\displaystyle h=0{,}6}$, ${\displaystyle m_{h}=0{,}98}$ et ${\displaystyle \varphi =180^{\circ }}$. Puis le champ augmente, sans variation de ${\displaystyle \varphi }$. Le même phénomène se répète dans la descende au niveau de l'inflexion de la courbe bleue.

Enfin, le cycle d’hystérésis n’est pas le même suivant l’orientation du champ ${\displaystyle H}$ par rapport à l’axe de facile aimantation. Plus ${\displaystyle \theta }$ est proche de 0°, plus le cycle est rectangulaire, et plus le champ nécessaire pour renverser l'aimantation est important. Plus ${\displaystyle \theta }$ est proche de 90°, plus il est facile de modifier l’aimantation avec le champ magnétique de manière progressive. La courbe dans le domaine de faible champ est presque linéaire et passe proche de 0.

L’allure de la boucle d'hystérésis est fortement dépendante de l’angle entre le champ magnétique et l’axe de facile aimantation. Si les deux sont parallèles (${\displaystyle \theta =0^{\circ }}$), la boucle d'hystérésis est la plus grande (avec ${\displaystyle m_{h}=h_{s}=1}$ en unités normales). L'aimantation commence parallèlement au champ et ne tourne pas jusqu’au moment où elle devient instable et se retourne dans la direction opposée. En général, plus l’angle est proche de 90°, plus la rotation devient réversible. Sur l’autre point extrême, à ${\displaystyle \theta =90^{\circ }}$, avec le champ perpendiculaire à l’axe de facile aimantation, il n’y a pas de saut. Pour un champ alternatif, l'aimantation tourne continuellement d'une direction à l’autre.

Pour un angle donné ${\displaystyle \theta }$, le champ de commutation est le point où la solution commute d’un minimum d’énergie (${\displaystyle \partial ^{2}\eta /\partial \varphi ^{2}>0}$) à un maximum (${\displaystyle \partial ^{2}\eta /\partial \varphi ^{2}<0}$). Ainsi, elle peut être calculée en résolvant l’équation 3 avec ${\displaystyle \partial ^{2}\eta /\partial \varphi ^{2}=0}$. La solution est

${\displaystyle h_{s}={{\sqrt {1-t^{2}+t^{4}}} \over 1+t^{2}}}$,

où

${\displaystyle t=\tan ^{1/3}(\theta )}$.

En unités normalisés, ${\displaystyle 0{,}5\leq h_{s}\leq 1}$^[1].

Une façon alternative de représenter le champ de commutation est de diviser le champ vectoriel ${\displaystyle h}$ à une composante ${\displaystyle h_{\parallel }=h\cos(\theta )}$, qui est parallèle à l’axe de facile aimantation, et une composante ${\displaystyle h_{\perp }=h\sin(\theta )}$, qui est perpendiculaire. Alors

${\displaystyle h_{\parallel }^{2/3}+h_{\perp }^{2/3}=1}$.

Si les composantes sont tracées en opposition, le résultat est un astroïde de Stoner-Wohlfarth. Une boucle d'hystérésis magnétique peut être calculée en appliquant une construction géométrique à cette astroïde^[4].

Stoner et Wohlfarth ont calculé le cycle d’hystérésis principal pour un système isotrope, constitué de particules identiques et orientées aléatoirement. Le résultat de ce calcul est reproduit sur la figure 5.

Pour ${\textstyle |h|<0{,}5}$, un changement réversible (flèche double) se produit : l'aimantation du système varie sur l’une des branches du cycle, en fonction de sa valeur initiale, et revient à ce même point lorsque l’on cesse de le soumettre au champ magnétique.

Pour ${\textstyle |h|>0{,}5}$, le changement est irréversible (flèche simple) : l'aimantation se renverse et passe sur l’autre branche du cycle, il est impossible pour elle de revenir à sa position initiale sans champ magnétique extérieur.

Deux valeurs importantes sont indiquées sur la figure :

• La rémanence à saturation normalisée, ${\displaystyle m_{rs}}$, correspond à la magnétisation résiduelle de l’échantillon lorsque l’on retire le champ magnétique appliqué.
• La coercivité ${\displaystyle h_{c}}$ correspond au champ magnétique pour lequel la magnétisation de l’échantillon est nulle.

La courbe rouge qui commence à l'origine est la courbe de première aimantation. Elle image le comportement d’un échantillon désaimanté lors de l'application d'un champ magnétique.

On considère que, lorsque l’on désaimante l’échantillon, on laisse à chaque moment magnétique une probabilité égale de s’orienter dans un sens ou l’autre de l’axe de facile aimantation. Le système devient donc une moyenne entre les branches haute et basse du cycle: sans champ h extérieur, il n’est pas aimanté. Lorsqu'on l'aimante, il suit une courbe correspondant à la moyenne des branches hautes et basses du cycle: une moitié des particules suit la branche haute tandis que l’autre suit la branche basse. Il est possible d’obtenir la même courbe pour l'aimantation opposée.

Une barrière de potentiel est définie comme l’énergie qui sépare deux minima.

En supposant que ${\textstyle \varphi }$ est tel qu'on se trouve dans un minimum d’énergie, on peut écrire la barrière énergétique sous la forme ${\textstyle \Delta E=(1-|h|)^{\beta }}$ où ${\textstyle \beta }$ va dépendre de l’angle ${\textstyle \theta }$ entre le champ appliqué et l'axe d'anisotropie^[2].

Dans la figure 7 on peut voir la variation de ${\textstyle \beta }$ en fonction de l’angle ${\textstyle \theta }$, ce qui est analogue à la variation de la barrière d’énergie.

On doit prendre en compte que ${\displaystyle 0<|h|<1}$, donc ${\textstyle 0<1-|h|<1}$. Ceci nous amène à dire qu'une augmentation de ${\textstyle \beta }$ entraîne une diminution de la barrière de potentiel.

Les fluctuations thermiques peuvent induire des orientations aléatoires dans une particule de Stoner. Si cette variation est suffisamment rapide par rapport au temps de mesure d’un cycle d'hystérésis, on observe un cycle moyenné.

Une méthode pour calculer ce cycle est de considérer qu’une particule de Stoner a plusieurs orientations qui font différents angles avec le champ appliqué^[2]. On redéfinit le système en 3D avec les angles représentés dans la figure 8.

Soit ${\textstyle p(\alpha ,\phi )}$ la fonction de densité de probabilité telle qu’elle soit uniforme pour ${\textstyle [0,\pi ]}$ et ${\textstyle [0,2\pi ]}$. La moyenne du cycle, c'est-à-dire la moyenne de la projection de l'aimantation le long de la direction du champ, est :

${\displaystyle {\overline {m_{p}}}={\iint \cos \left(\theta +\alpha \right)p\left(\alpha ,\phi \right)\sin \left(\alpha \right)\operatorname {d} \!\alpha \operatorname {d} \!\phi \over \iint p\left(\alpha ,\phi \right)\sin \left(\alpha \right)\operatorname {d} \!\alpha \operatorname {d} \!\phi }}$

Les fonctions de probabilité sont indépendantes, donc ${\textstyle p(\alpha ,\phi )=p(\alpha )p(\phi )}$. De plus on les définit uniformes, donc on retrouve :

${\displaystyle {\overline {m_{p}}}=\int _{0}^{\pi \over 2}\cos \left(\theta +\alpha \right)\sin \left(\alpha \right)\operatorname {d} \!\alpha }$

Donc en balayant ${\textstyle \alpha }$, on trouve l'angle ${\displaystyle \theta }$ qui minimise l'énergie du système.

Ensuite on réécrit :

${\displaystyle {\partial E \over \partial \theta }=\sin \left(\theta \right)\cos \left(\theta \right)+h\sin \left(\theta +\alpha \right)=0}$

Avec l'égalité ${\textstyle m=\cos(\theta +\alpha )}$ on retrouve :

${\displaystyle h=-m\cos \left(2\alpha \right)\pm {{2m^{2}-1} \over 2{\sqrt {1-m^{2}}}}\sin \left(2\alpha \right)}$

En balayant pour des valeurs de ${\textstyle m}$ on trouve les valeurs de ${\displaystyle h}$ qui satisfassent l’équation ${\textstyle \cos \left(2\alpha \right)+h\cos \left(\theta +\alpha \right)\geq 0}$. Ces valeurs correspondent bien aux minima d’énergie du système. On peut donc dessiner le cycle d’hystérésis 3D présent dans la figure 9.

Le modèle de Stoner-Wohlfarth est une approche “macro-spin” des systèmes magnétiques : c’est-à-dire que l’on considère que l’aimantation d’un grain monodomaine est en fait un seul moment magnétique géant, somme de tous les moments magnétiques portés par le grain. On utilise cette approche à cause de la complexité d’une description microscopique. Les matériaux magnétiques en général possèdent une structure multi-domaine, mais le modèle s'applique bien aux matériaux monodomaines tels que les nanoparticules où les matériaux composés de petits grains isolés électriquement de leurs voisins, de manière à les découpler magnétiquement.

Plusieurs méthodes existent pour compléter ce modèle :

• Les fluctuations thermiques : il est nécessaire de  prendre en compte les variations thermiques qui provoquent des sauts d’un état stable à un autre par-dessus une barrière énergétique.

• Les interactions entre particules : en ajoutant les interactions dipolaires entre particules au modèle de Stoner-Wohlfarth ou en prenant en compte le couplage d'échange entre des aimants.

Alors que le modèle de Stoner-Wohlfarth néglige l’influence de la température et donc du phénomène de relaxation, dans les travaux de Néel, ces effets sont mis en avant^[5].

Le modèle étendu inclut les possibilités d’une activation thermique et des fluctuations du moment magnétique d’une particule. Elle a été réalisée conformément à l'équation de Néel pour le taux de relaxation entre les minimas d'énergie locaux séparés par une barrière d'énergie ${\textstyle U_{0}}$ :

${\displaystyle P=p_{0}\exp \left(-{U_{0} \over k_{B}T}\right)}$,

où ${\textstyle p_{0}}$ est le taux de fluctuation, qui est légèrement dépendant de la température ${\textstyle T}$ et déterminé par les propriétés basiques de la particule en question. Par exemple, il peut être défini par la moyenne statistique des forces aléatoires fluctuant rapidement et exprimée en termes d'un «champ aléatoire».

Contrairement aux difficultés rencontrées lors du traitement des données expérimentales avec des modèles basés sur l’équation de Laudau-Lifshitz-Gilbert, le modèle étendu de Stoner-Wolfarth colle aux données expérimentales et permet d’estimer les caractéristiques physiques d’échantillons contenant des nanoparticules. Les modèles de Stoner-Wohlfarth et le modèle étendu de Stoner-Wohlfarth prédisent le comportement magnétique d’un système de particules idéal et est donc communément accepté comme référence.

Il est supposé qu’avec un champ magnétique changeant, le moment magnétique d’une particule (étant dans un minimum d’énergie) suit la position du minimum d’énergie local. Cependant le moment magnétique peut également changer instantanément sa direction par un saut au-dessus de la barrière énergétique séparant deux minima.

On suppose que, selon la force du champ magnétique à chaque instant, le procédé de relaxation est défini par deux paramètres :  ${\textstyle p_{ij}}$ et ${\textstyle U_{ij}}$.

${\displaystyle p_{12}(\theta ,H,T)={p_{0} \over 2}\sum _{i=1,2}\exp \left(-{U_{1i}(\theta ,H) \over k_{B}T}\right)}$

${\displaystyle p_{12}(\theta ,H,T)={p_{0} \over 2}\sum _{i=1,2}\exp \left(-{U_{2i}(\theta ,H) \over k_{B}T}\right)}$

${\displaystyle U_{ij}(\theta ,H)=E_{j}^{(max)}(\theta ,H)-E_{i}^{(min)}(\theta ,H)}$

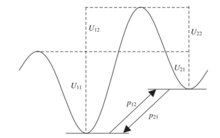
Ici, ${\textstyle p_{12}}$ et ${\textstyle p_{21}}$ donnent un sens aux probabilités des transitions entre les états d'équilibre locaux (voir schéma). Pour chaque groupe de particules avec différentes orientations, les valeurs de ${\textstyle E_{j}^{(max)}}$ et ${\textstyle E_{i}^{(min)}}$ peuvent être estimées au moyen de calculs numériques.

Dans les champs magnétiques où ${\textstyle |h|<H_{c}}$, chaque particule ne peut rester que dans deux états correspondant aux minima d'énergie locaux entre lesquels les transitions de relaxation peuvent se produire. Ensuite, les populations d'équilibre relatif des états sont définies par les principes d'équilibrage détaillés :

${\displaystyle \omega _{i}^{(0)}(\theta ,H,T)={\exp \left(-{E_{i}^{(min)}(\theta ,H) \over k_{B}T}\right) \over \exp \left(-{E_{1}^{(min)}(\theta ,H) \over k_{B}T}\right)+\exp \left(-{E_{2}^{(min)}(\theta ,H) \over k_{B}T}\right)}}$

La projection de l'aimantation à l'équilibre de la particule sur la direction du champ magnétique est déterminée par l'expression suivante :

${\displaystyle m^{(0)}(\theta ,H,T)=\omega _{1}^{(0)}(\theta ,H,T)m_{1}(\theta ,H)+\omega _{2}^{(0)}(\theta ,H,T)m_{2}(\theta ,H)}$,

où ${\textstyle m_{i}=M_{i}(\theta ,H)/M_{0}}$ sont les projections du moment magnétique normalisés de la particule dans la direction du champ magnétique correspondant aux minima d’énergie locaux.

On effectue la dérivée de la relation de relaxation de la magnétisation qui s’applique sur les populations des niveaux d’énergie du modèle de Stoner-Wohlfarth ${\textstyle \omega _{1}}$ et ${\textstyle \omega _{2}}$.

${\displaystyle {\operatorname {d} \!\omega _{1,2}(t) \over \operatorname {d} \!t}=\pm \left(p_{21}(t)\omega _{2}(t)-p_{12}(t)\omega _{1}(t)\right)}$

Sachant que ${\textstyle \omega _{1}(t)+\omega _{2}(t)=1}$,

${\displaystyle {\operatorname {d} \!{\tilde {\omega }}(t) \over \operatorname {d} \!t}=-p(t)\left({\tilde {\omega }}(t)-{\tilde {\omega }}^{(0)}(t)\right)}$

Avec la différence de population

${\displaystyle {\tilde {\omega }}(t)=\omega _{1}(t)-\omega _{2}(t)}$

et

${\displaystyle p(t)=p_{12}(t)+p_{21}(t)}$,

${\displaystyle {\tilde {\omega }}^{(0)}(t)=\omega _{1}^{(0)}(t)-\omega _{2}^{(0)}(t)}$.

L’équation différentielle est le modèle étendu de Stoner-Wohlfarth. En résolvant cette équation différentielle avec des conditions initiales, un certain nombre de phénomènes d'aimantation observés expérimentalement en fonction de la température, du temps et des champs magnétiques externes peuvent être compris et décrits quantitativement.

Les propriétés magnétiques théorisées par Stoner et Wohlfarth ont permis le développement de technologies utilisant l’hystérésis magnétique de certains matériaux. Comme par exemple le disque dur. Ce modèle est également très utilisé pour décrire les propriétés de nanoparticules magnétiques, et donc des ferrofluides.

• Critère de Stoner

• Stoner-Wohlfarth magnetization reversal app

• Portail des mathématiques
• Portail de la physique