La modélisation cinématique des mécanismes a pour objet la constitution d'un outil de calcul permettant de valider ou vérifier par le calcul les performances mécaniques d'un système. Le graphe des liaisons en est la forme la plus fondamentale. Le schéma cinématique donne quant à lui une représentation simplifiée permettant une meilleure compréhension du fonctionnement (aspect cinématique).
Mécanisme
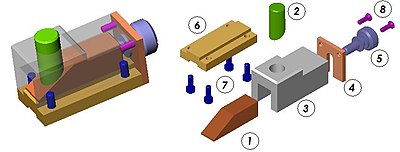
Un mécanisme est un ensemble organisé de pièces dans le but d'engendrer un effet souhaité. La modélisation cinématique a pour objectif la modélisation de cette organisation. Elle demande alors la définition des pièces et celle des liaisons mécaniques qui les agencent.
Pièces
À ce niveau de l'étude, on considère que des solides indéformables. Les premières études de performances reposent sur la mécanique du solide. Ce n'est que dans un deuxième temps que ces résultats sont interprétés pour le calcul de déformation ou résistance des pièces.
Les solides déformables, tel que ressorts ou courroies, font l'objet d'une considération particulière, et sont le plus souvent modélisés par une action extérieure, ou une liaison mécanique spécifique.
Classes d'équivalence
Il est courant dans un mécanisme de voir des pièces distinctes assemblées rigidement pour ne plus bouger pendant le fonctionnement. Par exemple une bielle monobloc ne peut être montée. Elle est donc constituée de deux parties rendues solidaires qui remplit la même fonction qu'une pièce unique. Ces sous-ensembles constituent des classes d'équivalence représentant une entité cinématique indépendante du mécanisme.
On les nomme parfois groupes cinématiques ou sous-ensemble cinématique.
Un peu de mathématiques
Dans un ensemble, une classe d'équivalence est un sous ensemble sur lequel s'applique une relation d'équivalence (réflexive, symétrique et transitive). Elle établit ainsi un lien entre les éléments présentant des propriétés communes.
Pour les mécanismes
La relation considérée est (R) = « est sans mouvement relatif possible avec »
En effet soit A, B et C trois pièces du mécanisme.
- On a forcément: A(R)A, B(R)B, C(R)C puisqu'il s'agit de corps indéformables (réflexivité).
- De plus, si A(R)B alors B(R)A (symétrie).
- Enfin, si A(R)B et B(R)C, alors A(R)C (transitivité).
les sous ensembles ainsi constitués sont en fait des groupes de pièces totalement solidaires les unes des autres pendant la phase de fonctionnement considérée. Cette distinction de phase est importante puisqu'on peut par exemple à propos d'une automobile s'intéresser à la chaîne de transmission de puissance vers les roues avant (direction supposée bloquée) ou au système de direction (véhicule arrêté). De même sur un mécanisme d'horlogerie, on pourra séparément analyser le mouvement des aiguilles en marche normale ou en phase de remise à l'heure.
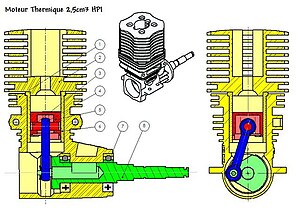
Pour déterminer les classes d'équivalence dans un mécanisme il existe plusieurs méthodes :
- la première, systématique, applicable sur un mécanisme comportant peu de pièces ( n pièces) consiste à vérifier toutes les relations i(R)j (i et j dans [1,n]).
- la deuxième plus intuitive, consiste, en partant des éléments d'assemblage (vis, boulons…), à déterminer les pièces solidaires. Cela est d'autant plus facile si on dispose — et c'est souvent le cas — d'un plan du système. Alors une bonne démarche est la mise en couleur de ce plan, en évitant de colorier les parties fixes (ou alors avec une couleur neutre) afin que les éléments mobiles ressortent mieux.
Liaison mécanique
Une liaison mécanique est une relation entre deux solides par contact. En réalité cette notion est étendue aux classes d'équivalence. Chaque liaison restreint l'espace des degrés de liberté des pièces du mécanisme. L'ensemble des liaisons d'un mécanisme et leur disposition relative dans l'espace constituent la définition de celui-ci. La seule définition des liaisons ne suffit pas. si, par exemple les gonds d'une porte sont placés au-dessus de celle-ci, elle devient basculante. Si les pivots de roues d'une automobiles ne sont pas parallèles, elle fonctionnera moins bien.
Liaisons élémentaires
L'article liaison (mécanique) donne la définition des 10 liaisons élémentaires constituant les mécanismes.
Autres liaisons
Les ressorts et autres éléments de transmission de mouvement seront considérés comme liaison technologique et feront l'objet d'une modélisation et d'une représentation spécifique.
Ressorts
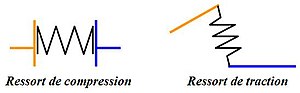
Les ressorts apparaissent sur le schéma cinématique sous forme d'une ligne en zigzag. On distingue cependant les ressorts de traction, qui sont accrochés, des ressorts de compression qui sont en appui.
Cependant, malgré sa représentation sur le schéma cinématique, un ressort n'est pas un solide indéformable. Il ne constitue donc pas une classe d'équivalence (voir illustration ci-contre). Le ressort a souvent un rôle de « maintien du contact ». Il peut être exclu du schéma ou représenté pour des raisons esthétiques ou explicatives.
Dans le graphe des liaisons, les ressorts sont indiqués sous forme d'une paire de forces opposées et de droite commune. Ils deviennent donc des efforts extérieurs. C'est souvent le modèle employé par les logiciels de calcul pour intégrer les ressorts (complété par la loi de comportement F=k.x).
Courroies, chaînes et engrenages
Ces éléments de transmission de puissance sont souvent représentés sous leur forme compilée bien plus claire que la liaison réellement mise en jeu (ponctuelle principalement). On peut les distinguer, par une ligne interrompue, sur le graphe des liaisons.
Crabots, verrous et embrayages

Ce sont des éléments technologiques qui permettent des liaisons temporaires. La modélisation cinématique raisonne, en général, sur des liaisons permanentes. C'est donc dans un contexte plus technologique que ces organes sont considérés.
Graphe des liaisons
- Note
- Il ne faut pas confondre le graphe des liaisons utilisé en génie mécanique avec celui utilisé en physique ; voir pour cela Graphe de liaisons.
Présentation du graphe des liaisons
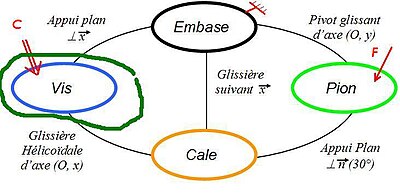
Il s'agit aussi d'un outil mathématique dont certaines propriétés s'accordent avec les propriétés de mécanisme. Il est constitué de sommets (ici des ellipses) représentant les classes d'équivalence et d'arcs représentant les liaisons.
On peut compléter ce graphe par les efforts extérieurs au mécanisme (en rouge sur l'exemple), afin d'en faire l'étude mécanique statique ou dynamique. Il porte alors le nom de graphe des actions mécaniques. Grâce à cet outil, on établit très rapidement le bilan des actions extérieures à tout sous-ensemble isolé. L'exemple de la vis dont la frontière d'isolement rencontre trois actions mécaniques (un couple et deux liaisons).
Alors il contient l'ensemble des éléments définissant le mécanisme. Certains logiciels de mécanique sont capables de le produire automatiquement à partir de la définition des classes et des liaisons, et de fournir une simulation de fonctionnement (Motionworks, méca3D, etc.).
Il existe également un graphe des liaisons non minimal. Dans ce cas on peut avoir plusieurs liaisons entre deux classes.
Pour des mécanismes élaborés, le graphe peut vite prendre une allure de sac de nœuds. Cependant, dans la plupart des cas on peut obtenir du premier coup un graphe clair et exploitable : un mécanisme présente en général une chaîne cinématique (éléments successivement entraînés depuis une pièce d'entrée jusqu'à une pièce de sortie). En plaçant au centre du graphe, la classe d'équivalence représentant le bâti du système, et en enroulant autour de celui-ci la (ou les ) chaînes cinématique évidente, on doit obtenir un graphe sur lequel on distinguera deux types de liaisons :
- en périphérie du graphe les liaisons intervenant dans la transmission du mouvement ;
- radialement (en le bâti et les éléments périphériques) les liaisons intervenant dans le guidage des pièces (sans transmission de puissance) ;
- très rarement, quelques liaisons complémentaires dont les raisons sont d'ordre technologique.
Propriétés du graphe
Nombre de cycles
Le nombre cyclomatique du graphe peut être calculé par la formule :
Il représente le nombre de cycles indépendants suivant lesquels on peut parcourir un chemin fermé. Si on applique les relations de composition des vitesses sur une boucle complète, ce qui revient à écrire des vecteurs nuls, on obtient pour chaque cycle, 6 équations algébriques dont les inconnues sont les paramètres de position de chaque liaison (degrés de liberté) auxquelles il faut retirer le nombre de mobilités du mécanisme (autant de degré pilotes).
Le graphe de la borne ci-dessus comporte 5-4+1=2 cycles indépendants qui nous fournissent 12 équations cinématiques vérifiées pour chaque position. Ce mécanisme comporte une mobilité, les degrés de liberté de l’ensemble des liaisons s’élèvent à 5 (-1) si on considère une vis liée par pivot (et 7(-1) si on considère le cas d’un appui plan). Dans les deux cas le nombre d’équations est suffisant ce qui signifie qu’il existe, pour chaque valeur du degré pilote, une solution unique (si elle existe) pour les positions relatives des pièces.
Graphes ouverts et fermés
Dans le cas d’un système sans cycle (nombre de cycle nul), la position de la pièce en bout de ligne peut être assurée de multiples manières. C'est le cas des bras de robots, ou des pieds support de lampe. Cette non-bijection est source de difficultés rencontrées en robotique, puisqu’à partir d’une position souhaitée (d’une pince par exemple), il faudrait déterminer les positions dans chaque liaison pour pouvoir commander les moteurs. Or la solution n'est pas unique, ce qui complique les algorithmes.
Exploitation du modèle
Lorsqu'on étudie le comportement d'un mécanisme, on s'intéresse en particulier aux mouvements relatifs ou absolus des pièces, aux efforts transmis dans les liaisons, et à la relation entre les deux.
- En statique, l'équilibre des pièces donnent les équations et les liaisons donnent les inconnues de liaison : le problème comprend a priori 6 équations par pièce et autant d'inconnues statiques indépendantes qu'il y a de degrés de liaison en tout.
- En cinématique, le mouvement des pièces donnent les inconnues (6 degrés de liberté ou simples paramètres cinématiques indépendants) et les liaisons donnent les équations : pour le problème on dispose alors de 6 inconnues par pièce et autant d'équations qu'il y a de degrés de liaison.
Schéma cinématique
Utilisation d'un schéma cinématique

On appelle schéma cinématique minimal celui qui représente un mécanisme avec au plus une liaison mécanique entre deux pièces ou classe d'équivalence.
On peut aussi dire que c'est une représentation d'un mécanisme qui met en évidence les possibilités de mouvements relatifs entre les groupes cinématiquement liés. Les liaisons sont positionnées dans l'espace en situation de fonctionnement. On ne représente ni les épaisseurs de pièces, ni les solutions technologiquement développées.
Il peut y avoir intérêt à décomposer une liaison, par exemple un pivot réalisé par deux roulements à billes assurant respectivement une liaison sphérique (rotule) et une liaison sphère-cylindre (linéaire annulaire). Cela permet alors, par le calcul de déterminer la part d'efforts subie par chacun des éléments alors que l'effort effectivement et globalement transmis par la liaison pivot est inexploitable.
Le schéma cinématique revêt deux fonctions principales en mécanique :
- aide à la conception en donnant le principe cinématique de fonctionnement ;
- aide à la compréhension du dispositif existant.
S'il est produit à l'échelle, il peut servir de fond d'esquisse dans des calculs de vitesses et forces.
Comment construire le schéma à partir du graphe des liaisons
Si le graphe des liaisons est complet et sans erreur, alors, contrairement aux idées reçues, l'exécution du schéma cinématique ne doit pas poser de problème :
- la définition des classes d'équivalence ;
- la définition des liaisons (nature, orientation, position).
La démarche de construction du schéma cinématique est la suivante :
- Recenser l'ensemble des points et axes caractéristiques (centre et directions des repères de liaison) et les placer sur le schéma dans des positions relatives conformes au mécanisme réel ;
- Placer aux endroits adéquats tous les symboles de liaison (orientation bien choisie) ;
- Relier par des traits continus les pattes d'accrochage de liaisons qui se rapportent à une même classe d'équivalence.
En appliquant cette démarche, le schéma est forcément juste même s'il n'est pas compréhensible. Paradoxe du schéma. Pour remédier à cela, on peut éventuellement :
- échanger deux classes d'équivalence sur une liaison ce qui peut éliminer certains nœuds ;
- respecter en général la notion de contenant/contenu (une pièce étant souvent emboîtée dans une autre) ;
- tracer des traits parallèles aux axes principaux du repère ;
- esquisser une forme réaliste pour les pièces constituant les entrées ou sortie du mécanisme ;
- adopter une couleur différente pour chaque classe d'équivalence.
Schéma technologique
Il est des cas, par exemple des robots très compacts avec beaucoup de liaisons coaxiales, où le schéma cinématique est impossible à réaliser de façon claire. Dans la mesure où le schéma n'est pas un outil de calcul mais de représentation, on a recours à une représentation moins normalisée, mais tout aussi explicite. Il n'y a donc pas de règles de construction.
Voir aussi
Bibliographie
- La série des normes ISO 3952 concernant les schémas cinématiques[1]
- la 4L de jacky, PCF, Caron Daniel, Jeay Emile, Lacage Bernard, Rea Jacky, Systèmes mécaniques (théorie et dimensionnement), Morizur, , 657 p. (ISBN 2-10-001051-4)
Articles connexes
En mécanique :
En mathématiques :
Liens externes
- « Tableau des liaisons », sur SciencesIndustrielles.com (consulté le ).











