Cet article est orphelin. Moins de trois articles lui sont liés (mars 2023).

Vous pouvez aider en ajoutant des liens vers [[Paradoxe du littoral]] dans les articles relatifs au sujet.

Cet article a une forme trop académique (mars 2023).

La forme ressemble trop à un extrait de cours et nécessite une réécriture afin de correspondre aux standards de Wikipédia. N'hésitez pas à l'améliorer.

Un exemple du paradoxe du littoral. Si le littoral de la Grande-Bretagne est mesuré en unités 100 kilomètres (62 mi) de long, alors la longueur du littoral est d'environ 2 800 km (1 700 mi). Avec 50 km (31 mi) unités, la longueur totale est d'environ 3 400 km (2 100 milles), environ 600 kilomètres (370 mi) de plus.

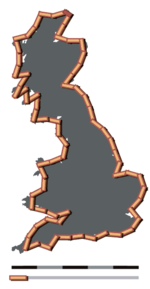
Le paradoxe du littoral est l'observation contre-intuitive que le littoral d'une masse continentale n'a pas de longueur définie. Cela résulte des propriétés apparentées à celles d'une courbe fractale des littoraux ; c'est-à-dire le fait qu'un littoral a typiquement une dimension fractale. Bien que le « paradoxe de la longueur » ait été précédemment noté par Hugo Steinhaus^[1], la première étude systématique de ce phénomène est réalisée par Lewis Fry Richardson^[2],[3], et il est développé par Benoît Mandelbrot^[4],[5].

La longueur mesurée du littoral dépend de la méthode utilisée pour le mesurer et du degré de généralisation cartographique. Une masse continentale ayant des caractéristiques à toutes les échelles, allant de centaines de kilomètres à de minuscules fractions de millimètre et moins, il n'y a pas de taille évidente de la plus petite caractéristique qui devrait être prise en considération lors de la mesure, et donc pas de périmètre unique bien défini à la masse continentale. Diverses approximations existent lorsque des hypothèses spécifiques sont faites sur la taille minimale des caractéristiques.

Le problème est fondamentalement différent de la mesure d'autres bords plus simples. Il est possible, par exemple, de mesurer avec précision la longueur d'une barre de métal droite et idéale en utilisant un appareil de mesure pour déterminer que la longueur est inférieure à une certaine quantité et supérieure à une autre quantité, c'est-à-dire la mesurer avec un certain degré d'incertitude. Plus l'appareil de mesure est précis, plus les résultats seront proches de la longueur réelle du bord. Lors de la mesure d'un littoral, cependant, la mesure plus proche n'entraîne pas une augmentation de la précision - la mesure ne fait qu'augmenter en longueur, contrairement à la barre métallique, il n'y a aucun moyen d'obtenir une valeur maximale pour la longueur du littoral.

Dans l'espace tridimensionnel, le paradoxe du littoral s'étend volontiers au concept de surfaces fractales, où l'aire d'une surface varie en fonction de la résolution de mesure.

Le concept de base de longueur provient de la distance euclidienne. En géométrie euclidienne, une ligne droite représente la distance la plus courte entre deux points. Cette ligne n'a qu'une longueur. À la surface d'une sphère, celle-ci est remplacée par la longueur géodésique (également appelée longueur du grand cercle), qui est mesurée le long de la courbe de surface qui existe dans le plan contenant les deux extrémités et le centre de la sphère. La longueur des courbes de base est plus compliquée mais peut également être calculée. En mesurant avec des règles, on peut approximer la longueur d'une courbe en ajoutant la somme des droites qui relient les points :

L'utilisation de quelques lignes droites pour approximer la longueur d'une courbe produira une estimation inférieure à la longueur réelle ; lorsque des lignes de plus en plus courtes (et donc plus nombreuses) sont utilisées, la somme se rapproche de la vraie longueur de la courbe. Une valeur précise pour cette longueur peut être trouvée en utilisant le calcul infinitésimal, la branche des mathématiques permettant le calcul de distances infiniment petites. L'animation suivante illustre comment une courbe lisse peut être affectée de manière significative à une longueur précise :

Toutes les courbes ne peuvent pas être mesurées de cette manière. Une fractale est, par définition, une courbe dont la complexité change avec l'échelle de mesure. Alors que les approximations d'une courbe lisse tendent vers une valeur unique à mesure que la précision de la mesure augmente, la valeur mesurée pour une fractale ne converge pas.

Cette courbe de Sierpiński (un type de courbe remplissante), qui répète le même motif à une échelle de plus en plus petite, continue d'augmenter en longueur. S'il est compris comme itérant dans un espace géométrique infiniment subdivisible, sa longueur tend vers l'infini. En même temps, la « superficie » délimitée par la courbe « converge » vers un chiffre précis — tout comme, de manière analogue, la superficie d'une île se calcule plus facilement que la longueur de son littoral.

Comme la longueur d'une courbe fractale diverge toujours vers l'infini, si l'on devait mesurer un littoral avec une résolution infinie ou quasi infinie, la longueur des plis infiniment courts du littoral s'additionnerait à l'infini^[6]. Cependant, ce chiffre repose sur l'hypothèse que l'espace peut être subdivisé en sections infinitésimales. La valeur de vérité de cette hypothèse - qui sous-tend la géométrie euclidienne et sert de modèle utile dans les mesures quotidiennes - est une question de spéculation philosophique et peut ou non refléter les réalités changeantes de l'« espace » et de la « distance » au niveau atomique (environ l'échelle du nanomètre).

Les côtes sont moins définies dans leur construction que les fractales idéalisées telles que l'ensemble de Mandelbrot, car elles sont formées par divers événements naturels qui créent des modèles de manière statistiquement aléatoire, tandis que les fractales idéalisées sont formées par des itérations répétées de séquences simples et formulées^[7].

Peu avant 1951, Lewis Fry Richardson, en recherchant l'effet possible de la longueur des frontières sur la probabilité de guerre, a remarqué que les Portugais rapportaient que leur frontière mesurée avec l'Espagne était de 987 km, mais les Espagnols l'ont signalé comme 1 214 km. C'est le début du problème du trait de côte, qui est une incertitude mathématique inhérente à la mesure de limites irrégulières^[8].

La méthode dominante pour estimer la longueur d'une frontière (ou d'un littoral) consistait à tracer n segments de ligne droite égaux de longueur ℓ avec des séparateurs sur une carte ou une photographie aérienne. Chaque extrémité du segment doit être sur la limite. En enquêtant sur les écarts dans l'estimation des frontières, Richardson a découvert ce que l'on appelle maintenant l'« effet Richardson » : la somme des segments augmente de manière monotone lorsque la longueur commune des segments diminue. En effet, plus la règle est courte, plus la bordure mesurée est longue ; les géographes espagnols et portugais utilisaient simplement des règles de longueur différente.

Le résultat le plus étonnant pour Richardson est que, dans certaines circonstances, lorsque ℓ s'approche de zéro, la longueur de la côte s'approche de l'infini. Richardson avait cru, sur la base de la géométrie euclidienne, qu'un littoral approcherait une longueur fixe, tout comme des estimations similaires de figures géométriques régulières. Par exemple, le périmètre d'un polygone régulier inscrit dans un cercle se rapproche de la circonférence avec un nombre croissant de côtés (et une diminution de la longueur d'un côté). Dans la théorie des mesures géométriques, une courbe lisse telle que le cercle qui peut être approximée par de petits segments droits avec une limite définie est appelée une courbe rectifiable.

Plus d'une décennie après que Richardson a terminé ses travaux, Benoit Mandelbrot a développé une nouvelle branche des mathématiques, la géométrie fractale, pour décrire des complexes non rectifiables dans la nature tels que le littoral infini^[9]. Sa propre définition de la nouvelle figure servant de base à son étude est^[10] :

« J'ai inventé fractal à partir de l'adjectif latin fractus. Le verbe latin correspondant frangere signifie « casser » : créer des fragments irréguliers. Il est donc judicieux ... qu'en plus de « fragmenté » ... fractus devrait également signifier « irrégulier ». »

Une propriété clé de certaines fractales est l'auto-similarité ; c'est-à-dire qu'à n'importe quelle échelle la même configuration générale apparaît. Un littoral est perçu comme des baies alternant avec des promontoires. Dans la situation hypothétique où un littoral donné a cette propriété d'auto-similarité, alors quelle que soit la taille d'une petite section de littoral est agrandie, un modèle similaire de baies et de promontoires plus petits superposés sur des baies et des promontoires plus grands apparaît, jusqu'aux grains de sable. À cette échelle, le littoral apparaît comme un fil momentanément changeant, potentiellement infiniment long, avec un agencement stochastique de baies et de promontoires formés à partir des petits objets à portée de main. Dans un tel environnement (par opposition aux courbes lisses) Mandelbrot affirme^[9] que « la longueur du littoral s'avère être une notion insaisissable qui se glisse entre les doigts de ceux qui veulent la saisir. »

Il existe différents types de fractales. Un littoral ayant la propriété énoncée se trouve dans « une première catégorie de fractales, à savoir des courbes dont la dimension fractale est supérieure à 1 ». Cette dernière déclaration représente une extension par Mandelbrot de la pensée de Richardson. La déclaration de Mandelbrot sur l'effet Richardson est la suivante^[11] :

${\displaystyle L(\varepsilon )\sim F\varepsilon ^{1-D},}$

où L, longueur du littoral, fonction de l'unité de mesure ε, est approximée par l'expression. F est une constante et D est un paramètre que Richardson a trouvé en fonction du littoral approximé par L. Il n'a donné aucune explication théorique, mais Mandelbrot a identifié D avec une forme non entière de la dimension de Hausdorff, plus tard la dimension fractale. La réorganisation de l'expression donne

${\displaystyle F\varepsilon ^{-D}\cdot \varepsilon ,}$

où Fε ^{− D} doit être le nombre d'unités ε nécessaires pour obtenir L. La ligne brisée mesurant une côte ne s'étend pas dans une direction et ne représente pas une zone, mais est intermédiaire entre les deux et peut être considérée comme une bande de largeur 2 ε. D est sa dimension fractale, comprise entre 1 et 2 (et typiquement inférieure à 1,5). Les côtes plus brisées ont un plus grand D, et donc L est plus long pour le même ε. D est d'environ 1,02 pour le littoral de l'Afrique du Sud et d'environ 1,25 pour la côte ouest de la Grande-Bretagne^[12]. Pour les rives des lacs, la valeur typique de D est de 1,28^[13] Mandelbrot a montré que D est indépendant de ε.

• Dispute de la frontière de l'Alaska
• Dimension fractale
• Trompette de Gabriel
• Paradoxe sorite
• Paradoxes de Zénon

• (en) David G. Post et Michael Eisen, How Long is the Coastline of Law? Thoughts on the Fractal Nature of Legal Systems, janvier 2000 (lire en ligne), « XXIX(1) ».
• (en) Benoit B. Mandelbrot, The Fractal Geometry of Nature, Macmillan, 1982, 25–33 (ISBN 978-0-7167-1186-5), « II.5 How long is the coast of Britain? »

• (en) Littoraux sur Fractal Geometry (éd. Michael Frame, Benoit Mandelbrot et Nial Neger ; maintenu pour Math 190a à l'Université de Yale) (page archivée)
• (en) L'Atlas du Canada – Littoral et littoral (page archivée)
• (en) Blog NOAA GeoZone sur la côte numérique (page archivée)

• Portail de la cartographie
• Portail de la géodésie et de la géophysique