Ne doit pas être confondu avec torseur.

En mathématiques, plus précisément en algèbre multilinéaire et en géométrie différentielle, un tenseur est un objet très général, dont la valeur s'exprime dans un espace vectoriel. On peut l'utiliser entre autres pour représenter des applications multilinéaires ou des multivecteurs. On pourrait abusivement considérer qu'un tenseur est une généralisation à n indices du concept de matrice carrée (la matrice possède un indice ligne et un indice colonne — un tenseur peut posséder un nombre arbitraire d'indices inférieurs, covariants, et d'indices supérieurs, contravariants, à ne pas confondre avec des exposants), mais la comparaison s'arrête là car une matrice n'est qu'un simple tableau de nombres qui peut être utilisé pour représenter des objets abstraits, alors que le tenseur est, comme les vecteurs et les applications multilinéaires, un objet abstrait dont les coordonnées changent lorsqu'on passe d'une représentation dans une base donnée à celle dans une autre base.

On peut envisager l'outil tenseur dans quatre types d'utilisation différentes :

• le cas simple, où on l'utilise pour ses capacités à représenter des objets algébriques complexes et où on n'a pas besoin des concepts de distances ni d'angles ; on n'introduira pas de produit scalaire, et dans ce cas les coordonnées covariantes représentent des objets de type application linéaire et les coordonnées contravariantes représentent des objets de type (multi-)vecteurs ;
• le cas où la base est orthonormée, et où il n'y a pas de différence entre coordonnées covariantes et contravariantes ;
• le cas où la base n'est pas orthonormée, et où le produit scalaire est défini par un tenseur métrique. Dans ce cas, le tenseur métrique permet de convertir les coordonnées covariantes en coordonnées contravariantes (et vice versa) ;
• le cas des espaces courbes de Riemann et plus tard, de la relativité générale, dans lesquels le tenseur métrique est en fait un champ de tenseurs appelé métrique riemannienne (resp Métrique pseudo-riemannienne) et qui dépend donc de la position.

Dans tous ces cas, le terme tenseur est souvent utilisé par extension, pour désigner un champ de tenseurs, c'est-à-dire une application qui associe à chaque point d'un espace géométrique un tenseur différent.

En physique, les tenseurs sont utilisés pour décrire et manipuler diverses grandeurs et propriétés physiques comme le champ électrique, la permittivité, les déformations, ou encore les contraintes.

La première utilisation de la notion et du terme de tenseur s'est faite dans le cadre de la mécanique des milieux continus, en relation avec la nécessité de décrire les contraintes et les déformations subies par les corps étendus, à partir de laquelle fut formalisée la mécanique rationnelle. En particulier, le tenseur des contraintes et le tenseur des déformations sont utilisés dans la science des constructions pour définir l'état de tension et de déformation en tout point d'une structure. Outre la mécanique des fluides et mécanique du solide, les tenseurs sont utilisés dans de nombreux autres domaines de la physique, tels que l'électromagnétisme. Ils sont également largement utilisés en relativité générale, pour décrire rigoureusement l'espace-temps comme variété courbe quadri-dimensionnelle.

Les tenseurs sont également utilisés en géométrie différentielle pour définir sur une variété différentielle les notions géométriques de distance, d'angle et de volume. Cela se fait par le choix d'un tenseur métrique, c'est-à-dire un produit scalaire défini sur l'espace tangent de chaque point. Grâce à ce concept, sont alors définies et étudiées les questions liées à la courbure de la variété. D'autres tenseurs, tels que le tenseur de Riemann et le tenseur de Ricci, sont des outils importants pour cette étude.

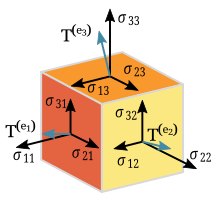
En mathématiques et en physique, un tenseur est un objet très général, défini intrinsèquement à partir d'un espace vectoriel ${\displaystyle V}$ (ou si on y ajoute un produit scalaire, à partir de l'espace euclidien, généralement tridimensionnel, ou bien quadri-dimensionnel) et qui ne dépend pas d'un système de coordonnées particulier. Cette notion physique de tenseur comme « objet indépendant du système de coordonnées » est utile pour exprimer beaucoup de lois physiques, qui par leur nature ne dépendent pas des systèmes de coordonnées choisis.

Par rapport à un système de coordonnées fixé, un vecteur de l'espace de dimension n s'exprime comme une suite finie de nombres (ce sont les composantes du vecteur), soit : un n-uplet. Si l'on change de système de coordonnées, ce vecteur s'exprimera alors par un autre n-uplet, différant selon une loi bien précise. Un tenseur, exprimé dans un système de coordonnées particulier, est une sorte de n-uplet généralisé qui peut avoir 1 dimension (un n-uplet), ou 2 (une matrice) ou plus. Par un changement du système de coordonnées, les composantes d'un tenseur, comme celles d'un vecteur, sont modifiées par une loi précise. Mais en soi, le vecteur, comme le tenseur, ne change pas.

Dans le langage de l'algèbre linéaire, la notion mathématique de tenseur est réalisée d'une manière plus rigoureuse par l'algèbre multilinéaire et la définition d'un tenseur peut être donnée sans faire référence aux systèmes de coordonnées (aux bases), en utilisant la notion d'application multilinéaire et d'espace vectoriel dual.

Le mot tenseur est issu de l'anglais d'origine latine tensor, mot introduit en 1846 par William Rowan Hamilton pour décrire la norme dans un système algébrique (finalement nommé algèbre de Clifford). Le mot a été utilisé avec son sens actuel par Woldemar Voigt en 1899.

Le calcul différentiel tensoriel a été développé vers 1890 sous le nom de calcul différentiel absolu, et fut rendu accessible à beaucoup de mathématiciens par la publication par Tullio Levi-Civita en 1900 du texte classique de même nom (en italien, suivi de traductions). Au XX^e siècle, le sujet devient connu sous le nom de analyse tensorielle, et acquiert une reconnaissance plus large avec l'introduction de la théorie de la relativité générale d'Albert Einstein, autour de 1915.

La relativité générale est complètement formulée dans le langage des tenseurs. Einstein a appris à les utiliser, avec quelque difficulté, avec l'aide du géomètre Marcel Grossmann ou peut-être de Levi-Civita lui-même. On utilise également les tenseurs dans d'autres domaines, par exemple la mécanique des milieux continus.

Un tenseur représente une application multilinéaire. L'algèbre des tenseurs est appelée algèbre tensorielle ou algèbre multilinéaire.

La définition des tenseurs exposée ici est la plus intrinsèque, parce qu'elle ne fait pas usage des bases, et est la plus utilisée en mathématiques.

Soit V un espace vectoriel de dimension n sur un corps commutatif ${\displaystyle K}$. L'espace dual V* est l'espace vectoriel formé de toutes les formes linéaires définies sur V. L'espace V* est aussi de dimension n. Les éléments de V et V* sont appelés respectivement vecteurs et covecteurs.

Un tenseur ${\displaystyle T}$ associe alors à h covecteurs ${\displaystyle {\vec {v}}_{1},\ldots ,{\vec {v}}_{h}}$ et k vecteurs ${\displaystyle {\vec {w}}_{1},\ldots ,{\vec {w}}_{k}}$ un scalaire

${\displaystyle T({\vec {v}}_{1},\ldots ,{\vec {v}}_{h},{\vec {w}}_{1},\ldots ,{\vec {w}}_{k}).\,\!}$

La multilinéarité garantit que la fonction est linéaire sur chaque variable.

L'ordre ou type ou valence du tenseur est le couple (h, k). On donne aussi le nom d'ordre ou de rang à la somme h+k.

Dans le cas où l'espace vectoriel V est de dimension finie n, on se donne une base de V ${\displaystyle ({\vec {e}}_{1},\dots ,{\vec {e}}_{n})}$ (avec les indices situés en bas), V* étant alors muni de la base duale, notée ici ${\displaystyle ({\vec {e}}^{\;1},\dots ,{\vec {e}}^{\;n})}$ (avec les indices notés en haut). Du fait de la multilinéarité, pour déterminer un tenseur T de type (h, k), il suffit de donner les valeurs qu'il prend lorsqu'on l'applique sur les vecteurs de base, autrement dit de donner les valeurs :

${\displaystyle T({\vec {e}}^{i},{\vec {e}}^{j},...,{\vec {e}}_{l},{\vec {e}}_{m},...)={T^{ij...}}_{lm...}}$

où les quantités ${\displaystyle {T^{ij...}}_{lm...}}$ possèdent h+k indices pouvant varier de 1 à n. Parmi ces indices, h sont conventionnellement notés en haut et k en bas. On appelle composante chacun des nombres ${\displaystyle {T^{ij...}}_{lm...}}$. Représenter un tenseur d'ordre h+k donné nécessite donc ${\displaystyle n^{h+k}}$ composantes.

La position des indices distingue ceux qui correspondent à un vecteur ou à un covecteur, en les disposant soit en haut, soit en bas. Un vecteur de V s'écrit ${\displaystyle x=\sum x^{i}{\vec {e}}_{i}}$, et les ${\displaystyle x^{i}={\vec {e}}^{\;i}(x)}$ s'appellent composantes contravariantes. Un vecteur de V* s'écrit ${\displaystyle y=\sum y_{i}{\vec {e}}^{\;i}}$, et les ${\displaystyle y_{i}=y({\vec {e}}_{i})}$ s'appellent composantes covariantes. De même, en ce qui concerne les composantes du tenseur, on mettra les indices en haut pour les contravariants, en bas pour les covariants. Par exemple, avec un tenseur du type (1,2), on posera ${\displaystyle T({\vec {e}}^{\;i},{\vec {e}}_{j},{\vec {e}}_{k})={T^{i}}_{jk}}$ pour chacune des ${\displaystyle n^{3}}$ composantes de T.

• Un tenseur d'ordre 0 est un scalaire. En effet, celui-ci est un simple nombre, qui ne dépend d'aucune base. Par exemple en mécanique classique masse, température, et autres quantités scalaires sont des tenseurs d'ordre 0.
• Un tenseur d'ordre 1 est assimilable à un vecteur ou à un covecteur. En effet, si l'espace V est de dimension n, un tenseur d'ordre 1 dispose de n composantes dans une base donnée, tout comme un vecteur. Si l'on change de base, les composantes changent, mais le tenseur ou le vecteur correspondant reste le même. En tant qu'application, le tenseur est une forme linéaire définie sur V ou sur V*, et est donc un élément de V* ou de V. Force, déplacement et autres quantités vectorielles sont des tenseurs d'ordre 1.
• Un tenseur d'ordre 2 est une forme bilinéaire. Une base étant choisie, cette forme est décrite par une matrice M et possède ${\displaystyle n^{2}}$ coefficients qui dépendent de la base de V. Le tenseur représente toutes les matrices obtenues à partir de M par changement de base.
• Plus généralement, on peut envisager des objets définis avec trois, quatre, ${\displaystyle m}$ indices ${\displaystyle \left(A_{ijk\ldots }\right)}$. Un objet défini par ${\displaystyle m}$ indices et vérifiant les formules de changement de base est un tenseur d'ordre ${\displaystyle m}$. Sur un espace vectoriel de dimension finie n, chaque indice peut prendre les valeurs de 1 à n. Un tenseur d'ordre m sur cet espace vectoriel a donc ${\displaystyle n^{m}}$ coefficients selon une base donnée. Par exemple, si le tenseur d'ordre ${\displaystyle m}$ représente une application multi-linéaire de V×V×… ×V dans ${\displaystyle \mathbb {K} }$, alors :

${\displaystyle \mathrm {T} ({\vec {a}}~,{\vec {b}}~,\ldots ,{\vec {l}}~)=\sum _{i,j,...,u}a^{i}b^{j}\ldots \ l^{u}\ \mathrm {T} (e_{i},e_{j},\ldots ,e_{u})}$

On retrouve les coefficients du tenseur T en identifiant ${\displaystyle \mathrm {T} _{ij\ldots u}=\mathrm {T} (e_{i},e_{j},\ldots ,e_{u})}$.

Si le tenseur « relie » ${\displaystyle m}$ espaces vectoriels de dimensions différentes ${\displaystyle n_{1},n_{2},...n_{m}}$, alors le tenseur contient ${\textstyle \prod _{i=1}^{m}n_{i}}$ coefficients.

Dans les notations, ${\displaystyle T_{ijk...}}$ représente la composante du tenseur T d'indices ${\displaystyle (i,j,k,...)}$. Quand on veut désigner un tenseur dans sa globalité tout en indiquant l'ordre de ce tenseur, on peut souligner le nom du tenseur d'autant de traits que l'ordre du tenseur. Ainsi, avec cette notation, un vecteur sera noté ${\displaystyle {\underline {u}}}$ plutôt que ${\displaystyle {\vec {u}}}$, et un tenseur de contraintes mécaniques (d'ordre 2) sera noté ${\displaystyle {\underline {\underline {\sigma }}}}$. Ceci est particulièrement utile quand on manipule des tenseurs d'ordres différents, ce qui est le cas en déformation élastique, pour laquelle on caractérise le comportement de déformation des matériaux par un tenseur ${\displaystyle {\underline {\underline {\underline {\underline {M}}}}}}$ d'ordre 4, et les déformations ${\displaystyle {\underline {\underline {\varepsilon }}}}$ et contraintes ${\displaystyle {\underline {\underline {\sigma }}}}$ par des tenseurs d'ordre 2. Dans le cas le plus simple de comportement élastique linéaire, ${\displaystyle {\underline {\underline {\sigma }}}={\underline {\underline {\underline {\underline {M}}}}}:{\underline {\underline {\varepsilon }}}}$.

Cette notation, utilisée en mécanique, n'est pas celle des mathématiques.

Dans les applications physiques, on distingue les indices matriciels, selon qu'ils sont contravariants (en les mettant en exposant) ou covariants (en les mettant en indice), en fonction du comportement de la grandeur tensorielle considérée face à des transformations linéaires de l'espace. La valence d'un tenseur est le nombre des indices matriciels associé au type de chacun d'eux ; des tenseurs de même ordre mais de valences différentes ne se comportent pas de la même façon lors de changement du système de coordonnées. Par ailleurs, un indice covariant peut être changé en indice contravariant par produit tensoriel contracté avec le tenseur métrique. On appelle cette opération élever ou abaisser des indices.

On note la valence en disant que le tenseur est de type (h, k) où h est le nombre d'indices contravariants et k le nombre d'indices covariants. La valence ne note pas l'ordre des indices. La valence est aussi utilisée quand on note le tenseur par une lettre, un indice en haut signifie alors que le tenseur est contravariant pour cet indice, un indice en bas signifie que le tenseur est covariant pour cet indice. On notera donc les vecteurs avec un indice haut, et les formes linéaires avec un indice bas. Ainsi :

• les vecteurs sont des tenseurs d'ordre 1 contravariants. Ils sont donc tenseurs de valence (1,0) ;
• les formes linéaires sont des tenseurs d'ordre 1 covariants. Ils sont de valence (0,1) ;
• pour le changement de base d'un tenseur (1,1), on aura une multiplication par la matrice de changement de base, et une multiplication par son inverse, exactement comme pour les matrices d'une application linéaire en algèbre linéaire. Un tenseur (1, 1) peut en effet être considéré comme une application linéaire. Soit T un tenseur (1,1) défini sur ${\displaystyle V^{*}\times V}$. À un couple (w, v) formé d'une forme linéaire w et d'un vecteur v, il associe un scalaire. Pour tout vecteur v, l'application qui à w associe T(w, v) et qui est notée T(., v) ou T(v) est alors une forme linéaire sur V*, c'est-à-dire un vecteur de V. Ainsi, T associe à un vecteur v un vecteur T(v). En outre, cette correspondance est linéaire ;
• pour le changement de base d'un tenseur (0,2), on aura deux multiplications par la matrice de changement de base, exactement comme pour les matrices d'une forme bilinéaire. Un tenseur (0, 2) est en effet une forme bilinéaire.

L'intérêt d'une telle notation, c'est qu'en cas de changement de base, elle donne directement le nombre de multiplications par la matrice de changement de base à effectuer : k, et par son inverse : h.

Une des utilisations des tenseurs concerne l'écriture d'équations qui soient indépendantes du système de coordonnées. Soit donc un premier système de coordonnées, utilisant une notation de contravariant, avec n vecteurs: ${\displaystyle Z=Z^{i}}$, i=1 à n; et un second système de coordonnées où les indices sont annotés d'une apostrophe, ${\displaystyle Z^{i'}}$. Le calcul permettant le passage d'un système à l'autre implique l'utilisation du Jacobien approprié, soit :

${\displaystyle Z^{i}=J_{i'}^{i}Z^{i'}}$

où la convention d'Einstein est utilisée, à savoir, il y a une sommation implicite sur l'indice répété quand il se trouve en contravariance (en haut) et en covariance (en bas). On peut également illustrer le jacobien comme une matrice où la ligne concernée est en contravariance (en haut) et la colonne concernée en covariance (en bas). Il faut également noter que la notation tensorielle permet de rejoindre les composants, individuellement, de la matrice, si bien qu'on peut écrire :

${\displaystyle Z^{i}=J_{i'}^{i}Z^{i'}=Z^{i'}J_{i'}^{i}}$

alors qu'avec la notation matricielle classique, on sait que le produit de deux matrices n'est pas symétrique, soit que A B diffère de B A, en général. La notation tensorielle permet de rétablir la symétrie de son algèbre.

De plus la notation nous permet de déterminer quel Jacobien utiliser selon quel système est l'original et lequel est le résultat du calcul. La sommation impliquée fait disparaître un des deux indices du Jacobien, c'est donc :

${\displaystyle Z^{i}=J_{i'}^{i}Z^{i'}}$ pour faire disparaître les apostrophes lors de la sommation implicite,

ou ${\displaystyle Z^{i'}=J_{i}^{i'}Z^{i}}$ pour calculer les sans-apostrophes.

Par contre, ${\displaystyle Z^{i}=J_{i}^{i'}Z^{i'}}$ est sans objet, ici, car non seulement l'indice i est de variance différente de chaque côté de l'égalité, mais surtout, l'expression n'implique pas de somme implicite car l'indice i' quoique répété n'est pas et en contravariance et en covariance, comme l'exige la convention d'Einstein pour qu'il y ait une somme implicite.

Avant de fournir la procédure pour calculer les Jacobiens, il nous semble approprié d'établir la règle des indices en contravariance et covariances, lorsqu'une dérivée est impliquée. Si l'on considère la division de deux fractions qui donne l'égalité ${\displaystyle (a/b)/(c/d)=a\,d/b\,c}$, lorsqu'une dérivée est impliquée avec la notation tensorielle, le résultat est tel que ${\displaystyle {\frac {\partial U_{j}^{i}}{\partial V_{m}^{k}}}=R_{jk}^{im}}$.

Il s'ensuit que pour le Jacobien ${\displaystyle J_{s'}^{s}}$, permettant de passer des s' aux s, on remarque, en comparant avec l'expression des fractions, que s joue le rôle de i, s' joue le rôle de k, et que j et m sont absents, donc ${\displaystyle J_{s'}^{s}={\frac {\partial Z^{i}}{\partial Z^{i'}}}}$

Donc non seulement la notation tensorielle nous permet de savoir quel Jacobien utiliser, mais quelles dérivées sont impliquées :

${\displaystyle J_{s'}^{s}={\frac {\partial Z^{i}}{\partial Z^{i'}}}}$ et non pas ${\displaystyle J_{s'}^{s}={\frac {\partial Z^{i'}}{\partial Z^{i}}}}$

On peut démontrer que les deux Jacobiens, ${\displaystyle J_{i'}^{i}}$ et ${\displaystyle J_{i}^{i'}}$ sont mutuellement l'inverse l'un de l'autre et ce, quel que soit le système de coordonnées initial ou final. En notation tensorielle, une telle relation peut être notée en utilisant le symbole de Kronecker :

${\displaystyle J_{i'}^{i}J_{j}^{i'}=\delta _{j}^{i}}$ où ${\displaystyle \delta _{j}^{i}}$ est égal à 1 si i=j, mais 0 autrement. À noter l'utilisation d'un indice additionnel, j, pour éviter une sommation additionnelle si on avait réutilisé i, au lieu de j.

Puisqu'on y est, considérons que ${\displaystyle \delta }$ est une matrice, alors ${\displaystyle \delta _{i}^{i}}$ est une sommation implicite car l'indice est répété en présence contravariante et covariante : ${\displaystyle \delta _{1}^{1}+\delta _{2}^{2}+\delta _{3}^{3}=1+1+1=3}$.

Notons également l'utilisation (dans un énoncé algébrique) du symbole de Kronecker pour "absorber" un indice en un autre : ${\displaystyle A_{i}\delta _{j}^{i}=A_{j}}$.

On définit un tenseur d'ordre 0 sous transformation, ou vrai scalaire, comme étant un scalaire qui, en plus d'être un scalaire, ne change pas de valeur (numériquement, compte tenu de ses unités) lorsqu'on change de système de coordonnées. Ainsi, une longueur entre deux points précis est un tenseur d'ordre 0. De même, la température en un point que je montre du bout de mon doigt ne change pas si je change le système de référence. Par contre, la distance de ce même point à l'origine est également un scalaire, mais la valeur numérique de ce scalaire change si je change d'origine. La distance à l'origine n'est donc pas un tenseur d'ordre 0 sous transformation. Quoique la distance à l'origine est un scalaire, elle n'est pas un vrai scalaire. Le mot "vrai", dans cette expression, n'a pas son sens du langage commun. On pourrait lui substituer l'adjectif "super", mais le précédent historique est d'utiliser le mot vrai, dans ce contexte tensoriel.

On définit un tenseur d'ordre 1 sous transformation, ou vrai vecteur, comme étant un vecteur qui, en plus d'être un vecteur, est relié linéairement par son Jacobien à ce même vecteur dans un autre système. ${\displaystyle U^{i}}$ est un tenseur d'ordre 1 sous transformation si pour un changement du système de coordonnées, on a ${\displaystyle U^{i'}=J_{i}^{i'}U^{i}}$. La position est un vecteur, mais pas un tenseur d'ordre 1 sous transformation, comme le montre le passage d'un système cartésien à un système de coordonnées polaires, cylindriques, ou sphériques. La vitesse, dérivée première de la position, est un tenseur d'ordre 1.

En physique, un exemple simple : considérons un bateau flottant sur l'eau. On veut décrire l'effet de l'application d'une force sur le déplacement du centre du bateau dans le plan horizontal. La force appliquée peut être modélisée par un vecteur, et l'accélération que subira le bateau par un autre vecteur. Ces deux vecteurs sont horizontaux. Mais leurs directions, qui devraient être identiques pour un objet circulaire (un solide de révolution autour d'un axe vertical, donc), ne le sont plus pour un bateau, qui est plus allongé dans un sens que dans l'autre. La relation entre les deux vecteurs, qui n'est donc pas une relation de proportionnalité, est cependant une relation linéaire, au moins si on considère une force petite. Une telle relation peut être décrite en utilisant un tenseur de type (1,1) (1 fois contravariant, 1 fois covariant). Un tel tenseur peut être considéré comme une application linéaire qui transforme un vecteur du plan (la force) en un autre vecteur du plan (l'accélération). Dans une base donnée, ce tenseur peut être représenté par une matrice, qui, lorsqu'on la multiplie par les composantes d'un vecteur, donne les composantes d'un autre vecteur. De la même manière que les nombres qui représentent un vecteur changent quand on change de système de coordonnées, les nombres qui représentent le tenseur dans la matrice changent quand le système de coordonnées change.

En mécanique, on peut également décrire les tensions, les forces intérieures subies par un solide ou un fluide par un tenseur. Le mot tenseur vient effectivement du verbe tendre, qui signifie soumettre à une tension. Considérons un élément de surface à l'intérieur du matériau ; les parties du matériau situées d'un côté de la surface exercent une force sur l'autre côté de la surface (et réciproquement). En général, cette force n'est pas orthogonale à la surface, mais dépendra linéairement de l'orientation de la surface. Nous pouvons la décrire par un tenseur d'élasticité linéaire, tenseur de type (2,0) (2 fois contravariant, 0 fois covariant), ou plus précisément, par un champ de tenseurs de type (2,0), puisque les forces de tension varient de point à point.

En dimension 3 pour simplifier, soit une base ${\displaystyle B({\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3})}$. Les composantes du vecteur ${\displaystyle {\vec {u}}}$ sont ${\displaystyle (u^{1},u^{2},u^{3})}$. Dans une autre base ${\displaystyle B'({\vec {e'}}_{1},{\vec {e'}}_{2},{\vec {e'}}_{3})}$, elles sont ${\displaystyle (u^{1'},u^{2'},u^{3'})}$. On cherche comment passer de l'une à l'autre des représentations.

Dans la base B, les vecteurs de la base B' s'écrivent :

${\displaystyle {\vec {e'}}_{j}={e^{1}}_{j}\cdot {\vec {e}}_{1}+{e^{2}}_{j}\cdot {\vec {e}}_{2}+{e^{3}}_{j}\cdot {\vec {e}}_{3}}$

On peut ainsi définir la matrice de changement de base P de B vers B' :

${\displaystyle P={\begin{pmatrix}{e^{1}}_{1}&{e^{1}}_{2}&{e^{1}}_{3}\\{e^{2}}_{1}&{e^{2}}_{2}&{e^{2}}_{3}\\{e^{3}}_{1}&{e^{3}}_{2}&{e^{3}}_{3}\end{pmatrix}}}$

Les colonnes de la matrice de changement de base sont les composantes des vecteurs de la nouvelle base dans l'ancienne. On a alors

${\displaystyle {\begin{pmatrix}u^{1}\\u^{2}\\u^{3}\end{pmatrix}}=P{\begin{pmatrix}u'^{1}\\u'^{2}\\u'^{3}\end{pmatrix}}}$ et

${\displaystyle {\begin{pmatrix}u'^{1}\\u'^{2}\\u'^{3}\end{pmatrix}}=P^{-1}{\begin{pmatrix}u^{1}\\u^{2}\\u^{3}\end{pmatrix}}}$.

Les nouvelles composantes s'obtiennent à partir des anciennes composantes par multiplication d'une seule matrice : le tenseur est dit d'ordre 1. En outre, cette matrice est l'inverse de la matrice de changement de base : ces composantes sont dites contravariantes.

Soit M une matrice représentant une application linéaire ƒ d'un espace vers un autre pour une base donnée dans chaque espace. On peut donc changer de base dans l'espace de départ et dans l'espace d'arrivée. Soient P et Q les matrices de changement de base respectivement dans l'espace de départ et dans l'espace d'arrivée. La matrice M' représentant ƒ pour les deux nouvelles bases est ${\displaystyle M'=Q^{-1}MP}$. Le changement de base se fait par multiplication de deux matrices de changement de base : le tenseur est dit d'ordre 2. L'une des matrices utilisées est la matrice de changement de base, l'autre est son inverse : le tenseur est du type (1,1).

Si M est la matrice d'une forme bilinéaire définie sur V, alors, après un changement de base de matrice de passage P, la nouvelle matrice est ${\displaystyle M'=^{\rm {t}}PMP}$. Le changement de base se fait par multiplication de deux matrices de changement de base : le tenseur est dit d'ordre 2. Les deux matrices sont relatives à P et nullement à son inverse : le tenseur est doublement covariant, du type (0,2).

Considérons une forme linéaire ƒ sur un espace V, de dimension 3 par exemple. Celle-ci associe à un vecteur u un scalaire

${\displaystyle f(u)=f_{1}u^{1}+f_{2}u^{2}+f_{3}u^{3}}$

Les indices relatifs aux composantes du vecteur sont notés en haut, ceux relatifs à la forme linéaire en bas. Considérons la base duale notée ici ${\displaystyle (e^{1},e^{2},e^{3})}$ constituée des formes linéaires telles que :

${\displaystyle e^{i}(e_{j})={\delta ^{i}}_{j}}$ (symbole de Kronecker)

soit

${\displaystyle e^{i}(e_{j})=1}$ si ${\displaystyle i=j}$

${\displaystyle e^{i}(e_{j})=0}$ sinon

La forme linéaire s'écrit alors:

${\displaystyle f=f_{1}e^{1}+f_{2}e^{2}+f_{3}e^{3}}$

et l'on a :

${\displaystyle f(u)={\begin{pmatrix}f_{1}&f_{2}&f_{3}\end{pmatrix}}\cdot {\begin{pmatrix}u^{1}\\u^{2}\\u^{3}\end{pmatrix}}}$

Si l'on fait un changement de base de l'espace V au moyen de la matrice de passage P, alors les composantes du vecteur u dans la nouvelle base sont

${\displaystyle P^{-1}{\begin{pmatrix}u^{1}\\u^{2}\\u^{3}\end{pmatrix}}}$

En revanche, les composantes de ${\displaystyle f}$ dans la nouvelle base duale sont

${\displaystyle {\begin{pmatrix}f_{1}&f_{2}&f_{3}\end{pmatrix}}P}$

On voit que dans le cas du changement de la base de formes linéaires, on multiplie par la matrice de changement de base, alors que dans le cas du changement de la base de vecteurs, on multiplie par son inverse. Le tenseur associé à une forme linéaire est d'ordre 1, covariant, donc du type (0,1).

La somme de deux tenseurs de même ordre et même valence est un tenseur de même ordre et de même valence que les deux tenseurs de départ, obtenu en sommant les composantes de deux tenseurs. Par exemple, dans le cas de tenseurs T et U d'ordre 2, ${\displaystyle ({\underline {\underline {T}}}+{\underline {\underline {U}}})_{ij}}$ = ${\displaystyle {\underline {\underline {T}}}_{ij}+{\underline {\underline {U}}}_{ij}}$.

Le produit d'un tenseur et d'un scalaire est un tenseur de même ordre et de même valence que le tenseur de départ, obtenu en multipliant les composantes du tenseur par le scalaire.

L'ensemble des tenseurs d'ordre et de valence donnés forment donc un espace vectoriel.

Le produit tensoriel entre ${\displaystyle T}$ d'ordre n, et ${\displaystyle U}$ d'ordre p produit un tenseur d'ordre n+p. Les n premiers indices sont repris de T, et les p indices suivants sont repris à partir de U. Leur valence est la même que l'indice dont ils proviennent. Chaque composante du résultat est le produit :

• de la composante de T associée aux n premiers indices de la composante du résultat
• de la composante de U associée aux p derniers indices de la composante du résultat.

Ainsi, le produit tensoriel du tenseur ${\displaystyle {T^{i}}_{j}}$ par le tenseur ${\displaystyle U_{kl}}$ est le tenseur d'ordre 4 ${\displaystyle {T^{i}}_{j}U_{kl}}$.

Exemples :

• Si on représente deux formes linéaires f et g par deux tenseurs (donc tenseurs d'ordre 1 et covariants), alors le produit tensoriel des deux tenseurs représente une forme bilinéaire, linéaire par rapport à chacune des variables des formes linéaires de départ, définie par : ${\displaystyle (u,v)\to f(u)g(v)}$. La notion de produit tensoriel provient donc directement de la notion de produit de fonctions.
• Si on multiplie par le produit tensoriel, un vecteur u et une forme linéaire f, le résultat sera un tenseur d'ordre (1,1), à savoir l'endomorphisme définie par ${\displaystyle v\to f(v)u}$. Si les composantes de u dans une base sont les ${\displaystyle u^{i}}$ et les composantes de f dans la base duale sont les ${\displaystyle f_{j}}$, alors les composantes de la matrice de l'endomorphisme précédent sont les ${\displaystyle u^{i}f_{j}}$. Cette matrice étant de rang inférieur ou égal à 1, ceci met en évidence qu'il existe de nombreux tenseurs d'ordre élevé qui ne sont pas le résultat du produit tensoriel.

Soit A et B deux matrices carrées représentant dans une base donnée deux tenseurs de type (1,1), de terme général respectif ${\displaystyle A_{j}^{i}}$ et ${\displaystyle B_{j}^{i}}$. Le produit matriciel C = AB représente un tenseur (1,1) de terme général ${\displaystyle C_{j}^{i}=\sum _{k}A_{k}^{i}B_{j}^{k}}$. On a réalisé la contraction du produit tensoriel des deux tenseurs (qui a pour terme général ${\displaystyle A_{k}^{i}B_{j}^{k}}$) et qui est de type (2,2) en prenant un indice commun, covariant pour l'un, contravariant pour l'autre. De même, un tenseur peut avoir des composantes covariantes et contravariantes, et quand on fait le produit contracté de deux indices, on le fait toujours entre composantes covariantes et contravariantes, ce qui explique que certains indices soient notés en haut et d'autres en bas, par exemple T_a^bc.

Le contracté d'un tenseur sur deux indices i et j, l'un étant covariant et l'autre contravariant est un tenseur d'ordre n-2 où n est l'ordre du tenseur de départ. Les indices i et j ont disparu dans le tenseur résultat ; la valence des autres indices est inchangée.

${\displaystyle T^{a}={T^{ac}}_{c}}$

Ici on a fait la somme sur toutes les valeurs possibles des deuxièmes et troisièmes indices, quand ceux-ci sont égaux.

Dans l'exemple ci-dessus, du produit tensoriel entre un vecteur et une forme linéaire de terme général ${\displaystyle u^{i}f_{j}}$, la contraction du tenseur résultant nous donne le résultat de l'application de la forme linéaire au vecteur, à savoir ${\displaystyle \sum _{i}u^{i}f_{i}}$.

On voit ici que le produit tensoriel est un moyen de combiner deux objets tout en préservant l'ensemble de leurs propriétés et en différant certaines opérations (ie. les objets restent plus ou moins séparables, si ce n'est que le produit tensoriel d'objets qui étaient déjà combinés peut être décomposé de plusieurs façons). La contraction par contre, revient à appliquer des opérations qui avaient été laissées en suspens.

Le produit tensoriel contracté entre ${\displaystyle A}$ d'ordre n, et ${\displaystyle B}$ d'ordre p, est un tenseur d'ordre (n+p-2). Les n-1 premiers indices proviennent de A (leurs valences respectives sont les mêmes que les n-1 premiers indices de A), les p-1 derniers proviennent de B (leurs valences respectives sont les mêmes que les p-1 derniers indices de B). Le produit tensoriel contracté est un produit tensoriel suivi d'une contraction entre l'indice n et l'indice n+1 du tenseur d'ordre n+p.

Une généralisation de ce produit contracté est le double-produit contracté (dont le résultat est un tenseur d'ordre n+p-4), le triple-produit contracté (dont le résultat est un tenseur d'ordre n+p-6), etc. De manière générale, le p-produit contracté définit un produit scalaire pour l'espace vectoriel des tenseurs d'ordre p. Le double-produit contracté est notamment très utilisé pour décrire la déformation élastique des matériaux.

On adopte souvent la convention de notation d'Einstein qui consiste à supprimer le signe de sommation et à le considérer comme implicite dès lors que l'indice est répété en haut et en bas dans une expression, par exemple

${\displaystyle \sum _{j}T_{i}^{j}u_{j}}$ et ${\displaystyle \sum _{j}T_{j}^{i}f^{\ j}}$

se notent respectivement

${\displaystyle T_{i}^{j}u_{j}}$ et ${\displaystyle T_{j}^{i}f^{\ j}}$

Avec cette convention, les expressions relatives au produit contracté de deux tenseurs, se noteront de façon simple. Ainsi, le produit des deux matrices de terme général ${\displaystyle A_{j}^{i}}$ et ${\displaystyle B_{j}^{i}}$ est la matrice de terme général ${\displaystyle A_{k}^{i}B_{j}^{k}}$.

La notation d'Iverson APL permet également de noter de façon concise les tenseurs et leurs opérations : produit tensoriel (∘.), contraction (/), produits scalaires, etc., en nombre réels, complexes et, dans certaines implémentations comme NARS2000, quaternions et octonions (voir l'article « APL (langage) »).

Le produit scalaire entre les vecteurs définit les notions de norme et d'orthogonalité. Il n'est pas nécessaire mais ajoute des outils très intéressants au calcul tensoriel. Dans une base orthonormée, il a une forme canonique simple qui consiste à multiplier une par une les composantes correspondantes des deux vecteurs; comme on exprime alors les produits contractés entre composantes covariantes et contravariantes, on doit ajouter entre les deux vecteurs une application bilinéaire qui permet de convertir les composantes contravariantes en composantes covariantes (ou le contraire). On a, dans le cas d'une base orthonormée ${\displaystyle {\vec {1}}_{i}}$ :

${\displaystyle {\vec {x}}\cdot {\vec {y}}=x^{i}{\vec {1}}_{i}\cdot {\vec {1}}_{j}y^{j}=x^{i}\delta _{ij}y^{j}}$.

Dans la plupart des cas, cependant, la base n'est pas orthonormée, et peut se représenter comme une transformation P de la base canonique. On a donc :

${\displaystyle {\vec {x}}=x^{i}{\vec {1}}_{i}}$, et

${\displaystyle {\vec {x}}={x_{e}}^{j}{\vec {e}}_{j}}$ avec ${\displaystyle {\vec {e}}_{j}=P_{j}^{k}{\vec {1}}_{k}}$

Il en résulte que

${\displaystyle {\vec {x}}\cdot {\vec {y}}={x_{e}}^{i}{\vec {e}}_{i}\cdot {y_{e}}^{j}{\vec {e}}_{j}={x_{e}}^{i}P_{i}^{k}{\vec {1}}_{k}\cdot {\vec {1}}_{l}P_{j}^{l}{y_{e}}^{j}={x_{e}}^{i}P_{i}^{k}\delta _{kl}P_{j}^{l}{y_{e}}^{j}={x_{e}}^{i}g_{ij}{y_{e}}^{j}}$ avec ${\displaystyle g_{ij}=P_{i}^{k}\delta _{kl}P_{j}^{l}}$

La nouvelle matrice ${\displaystyle g_{ij}}$ définit le produit scalaire dans la nouvelle base E, et s'appelle le tenseur métrique de l'espace avec la base E. Comme ${\displaystyle g_{ij}}$ est défini en multipliant ensemble le premier et le second indice de P, il est automatiquement symétrique.

Un indice haut peut être changé en un indice bas par multiplication avec le tenseur métrique, ${\displaystyle g_{ab}}$

${\displaystyle T_{ac}=g_{ab}T_{c}^{b}}$

(On utilise la convention d'Einstein, le signe somme sur l'indice b est sous-entendu)
Le résultat est un tenseur de même ordre mais de valence différente : un indice contravariant est devenu covariant dans le tenseur résultat.

Un indice bas peut être changé en indice haut par multiplication avec le tenseur métrique inverse ${\displaystyle g^{ab}}$ :

${\displaystyle {T^{a}}_{c}=g^{ab}T_{bc}}$

Le résultat est un tenseur du même ordre mais de valence différente : un indice covariant est devenu contravariant dans le tenseur résultat.

Le gradient d'un champ de tenseurs d'ordre n est la différentielle de ce champ. On obtient un champ de tenseurs d'ordre n+1. Les n premiers indices ont la même valence que le tenseur de départ. L'indice supplémentaire est covariant.

La divergence d'un tenseur d'ordre n est le produit tensoriel doublement contracté entre la différentielle de ce tenseur (autrement dit son gradient) et le tenseur métrique. On obtient alors un tenseur d'ordre n−1. L'indice manquant est contravariant.

Dans le cas de l'ordre 2, un tenseur peut être symétrique ou antisymétrique (ou ni l'un, ni l'autre).

Pour un tenseur symétrique, on a la relation T_ab = T_ba.

Pour un tenseur antisymétrique, on a la relation T_ab = -T_ba.

En général, un tenseur n'est ni symétrique, ni antisymétrique. Un tenseur quelconque peut cependant être décomposé en une partie symétrique S et une partie antisymétrique A, avec les relations :

• S_ab = (T_ab + T_ba)/2
• A_ab = (T_ab - T_ba)/2

Les parties symétriques et antisymétriques réunies rassemblent autant d'information que le tenseur originel.

Cette règle peut être étendue aux tenseurs d'ordre quelconque. On dira alors que le tenseur est symétrique pour une paire d'indices, s'il est invariant par échange des deux indices, et qu'il est antisymétrique pour une paire d'indices s'il se transforme en son opposé par échange des deux indices.

Les indices de la paire considérée doivent avoir même valence. (Dans le cas contraire la propriété de symétrie dépendrait de la base choisie).

Dans le cas particulier d'un espace vectoriel de dimension 3, un tenseur antisymétrique d'ordre 2 porte le nom de pseudovecteur.

Un tenseur est symétrique s'il est inchangé par des permutations des indices hauts ou une permutation des indices bas. Un tenseur d'ordre (0,2) ou bien (2,0) est symétrique si et seulement si ses composantes forment une matrice symétrique. Le fait pour un tenseur d'être symétrique ne dépend pas de la base choisie.

Un tenseur est antisymétrique si, par une permutation quelconque des indices, il subit un changement de signe qui est le signe de la permutation. Un tenseur d'ordres (0,2) ou (2,0) est antisymétrique si et seulement si ses composantes forment une matrice antisymétrique. Pour un tenseur antisymétrique, les composantes dans lesquelles un indice se répète au moins deux fois sont toutes nulles. Par exemple, dans un espace de dimension n, les n composantes ${\displaystyle T_{iij}}$ du tenseur ${\displaystyle T_{abc}}$ sont nulles. De ce fait, un tenseur de type (h, k) avec k>n ou h>n est nécessairement nul, parce que l'on ne peut avoir k (ou h) valeurs différentes dans {1, ..., n}. En outre (à une multiplication par un scalaire près), il existe un seul tenseur antisymétrique d'ordre (0,n) : le déterminant, ou tenseur de Levi-Civita.

Les tenseurs antisymétriques sont utilisés pour construire les formes différentielles.

• Claude Semay, Bernard Silvestre-Brac, Introduction au calcul tensoriel, Applications à la physique, Dunod, 2007, (ISBN 978-2-10-050552-4)

• Mécanique : tenseurs 1^re partie
• Éléments d'algèbre et d'analyse tensorielle à l'usage des mécaniciens
• Algèbre et analyse tensorielle pour l'étude des milieux continus
• Initiation aux Tenseurs
• Cours de Relativité Générale, d'après (en) Lecture notes on General relativity de Sean M. Carroll : traduction et adaptation par Jacques Fric

v · m Algèbre linéaire générale
Vecteur Scalaire Combinaison linéaire Espace vectoriel Matrice
Famille de vecteurs	Famille génératrice Famille libre (indépendance linéaire) Base Théorème de la base incomplète Théorème de la dimension pour les espaces vectoriels Rang Colinéarité
Sous-espace	Sous-espace vectoriel Somme de Minkowski Somme directe Sous-espace supplémentaire Dimension Codimension Droite Plan Hyperplan
Morphisme et notions relatives	Application linéaire Noyau Conoyau Lemme des noyaux Pseudo-inverse Théorème de factorisation Théorème du rang Équation linéaire Système d'équations linéaires Élimination de Gauss-Jordan Forme linéaire Espace dual Orthogonalité Base duale Endomorphisme linéaire Valeur propre, vecteur propre et espace propre Projecteur Symétrie Matrice diagonalisable Diagonalisation Endomorphisme nilpotent
Dimension finie	Espace vectoriel de dimension finie Trace Déterminant Polynôme caractéristique Polynôme d'endomorphisme Théorème de Cayley-Hamilton Polynôme minimal d'un endomorphisme Invariants de similitude Réduction d'endomorphisme Réduction de Jordan Décomposition de Dunford Décomposition de Frobenius
Enrichissements de structure	Norme Produit scalaire Forme quadratique Espace vectoriel topologique Orientation Algèbre sur un corps Algèbre de Lie Complexe différentiel
Développements	Théorie des matrices Représentation de groupe Analyse fonctionnelle Algèbre multilinéaire Module sur un anneau

v · m Tenseurs
Mathématiques	Tenseur en mathématiques Produit tensoriel Produit tensoriel de deux modules Produit tensoriel de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel Notation en indice abstrait
Physique	Convention de sommation d'Einstein Covariant et contravariant Tenseur métrique Tenseur énergie-impulsion Tenseur de Riemann Tenseur de Ricci Tenseur d'Einstein Tenseur de Weyl Tenseur de Levi-Civita Tenseur de Killing Tenseur de Killing-Yano Tenseur de Bel-Robinson Tenseur de Cotton-York Tenseur électromagnétique Tenseur des contraintes Tenseur des déformations

• Portail de la physique
• Portail des mathématiques