Le torseur des actions mécaniques, parfois abusivement appelé torseur statique, est largement utilisé pour modéliser les actions mécaniques lorsqu'on doit résoudre un problème de mécanique tridimensionnelle en utilisant le principe fondamental de la statique. Le torseur des actions mécaniques est également utilisé en résistance des matériaux. On utilisait autrefois le terme de dyname[1].
Approche « empirique »
Une action mécanique est représentée par une force, ou une répartition de forces créant un couple. Une action de contact — effet d'une pièce sur une autre — peut se décrire localement par une force et/ou un couple ; force comme couple sont des grandeurs vectorielles, elles ont chacune trois composantes par rapport au repère lié au référentiel de l'étude, supposé galiléen. On peut donc décrire une action de contact par un tableau de six nombres, les six composantes des vecteurs. Toutefois, l'effet d'un bras de levier fait que la force contribue à « l'effet de couple » de l'action ; il faut donc préciser le point d'application de la force.
Pour résoudre un problème de statique ou de dynamique du solide, il faut calculer le moment de toutes les forces par rapport à un même point. Avec le formalisme des torseurs, on parle de « transporter les torseurs » en un même point. Lorsque l'on transporte le torseur, la première colonne (composantes X, Y, Z) ne change pas, mais la seconde (L, M, N) est modifiée par le moment de la force.
On utilise les termes de :
- torseur d'action pour désigner le torseur des actions mécaniques décrivant l'action mécanique d'une pièce sur une autre, voir Liaison mécanique » Statique et dynamique ;
- torseur de cohésion ou torseur des efforts intérieurs pour désigner le torseur des actions mécaniques décrivant un effort interne à une pièce (résistance des matériaux), voir Principe de la coupure.
Définition
Soit une force appliquée en un point A. En un point B quelconque de l'espace, il est possible de définir un vecteur moment de cette force, .
Par construction, le champ des moments est équiprojectif, c'est donc un torseur des actions mécaniques.
La force représente une interaction entre deux corps. Le torseur est une représentation de l'effet mécanique de l'interaction. Si les corps sont appelés i et j, l'action de j sur i est habituellement notée « j/i » ou bien « j → i ». Le champ des moments est donc noté ou bien .
Deux torseurs peuvent-être décrits:
- le torseur équivalent : qui est la réduction du système de force en une force résultante et un moment résultant.
- le torseur résultant : qui est la réduction du système de force en une force résultante, correctement positionnée afin de tenir compte du moment résultant. Ce type de torseur est applicable uniquement dans le cas de système de force coplanaire ou si les lignes d'actions du moment résultant et de la résultante sont perpendiculaires dans le cas d'un système de force dans l'espace.
Résultante
Par construction, la résultante du torseur est le vecteur force.
La résultante est habituellement notée ou bien .
Éléments de réduction
Considérons une pièce 1 et une pièce 2 ayant un contact. Le torseur d'action de 2 sur 1 est noté
où la résultante représente la force exercée par le solide 2 sur le solide 1 et où le moment représente le moment exercé par le solide 2 sur le solide 1 au point A.
Ce torseur peut s'écrire en n'importe quel point. Le point A où l'on choisit de définir le moment est appelé « centre de réduction ».
Si l'on se place dans un repère , on peut décrire les vecteurs par leurs composantes :
et les éléments de réduction du torseur s'écrivent alors soit sous la forme vectorielle
soit sous la forme d'un tableau de six nombres
avec X, Y et Z en newton (N) et L, M et N en newton mètre (N m).
Le changement de centre de réduction d'un point A à un point B revient à calculer le moment de la résultante force par rapport à un point B ; cette opération est appelée « transport du torseur en B ». Si l'on connaît le moment de la force par rapport à un point A (habituellement le point d'application de la force, puisque le moment y est nul), on a :
Cas particuliers
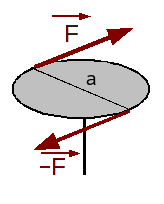
Un torseur dont la résultante est nulle est dit torseur couple: du fait de la relation de transport des moments, il est clair que pour tous points A et B, le moment d'un couple est indépendant du point de réduction choisi.
Le torseur dont le moment et la résultante sont nuls est appelé le torseur nul {0}.
Lorsque le moment est perpendiculaire à la résultante en un certain point, il l'est en tout point par la relation de transport des moments. On dit alors que ce torseur est un glisseur :
- ;
il existe une droite parallèle à la résultante telle que la réduction de ce torseur en tout point de cette droite a un moment nul. Les torseurs représentant des forces seules sont des glisseurs ; la droite sur laquelle le moment s'annule est la droite d'action de la force, elle contient le point d'application de la force.
Torseur d'action mécanique des liaisons parfaites
Un contact entre deux pièces 1 et 2 fait en général intervenir une distribution de forces : la zone de contact réelle est une surface Σ d'aire non nulle, on peut donc définir une densité de force en chaque point de la surface.
Le torseur représentant l'action de contact est la somme de tous ces torseurs :
où dS est un élément de surface infinitésimal autour du point M.
La résultante de ce torseur est la somme des forces :
Au point de contact, une pièce ne peut transmettre un effort à une autre que si le mouvement relatif est bloqué. Dans le modèle des liaisons parfaites, on ne considère que la transmission d'effort par obstacles, il n'y a pas de frottement.
En génie mécanique, les différents types de contact sont décrits par 12 liaisons mécaniques modèle, définies par la norme ISO 3952-1. Une liaison mécanique bloque certaines translations et certaines rotations relatives. On peut donc connaître la forme qu'aura le torseur d'action réduit au point de contact si l'on connaît la liaison entre les pièces. Selon le type de liaison, certaines composantes du torseur d'action seront nulles. On parle de torseur des actions mécaniques transmissibles (TAMT).
Ceci est résumé dans le tableau ci-dessous.
Il convient de souligner que l'emplacement des zéros dépend de l'orientation de la liaison par rapport aux axes du repère. En particulier, il n'y a a priori aucune raison pour que les vecteurs caractéristiques de la liaison — normale de contact, ligne de contact — soient parallèles aux axes du repère général ; dans ces cas-là, il importe de préciser le repère local utilisé, puis d'effectuer un changement de repère pour pouvoir utiliser ce torseur avec les autres.
Notes et références
- G. Lemasson, J. Gal, Mécanique, 1. Statique et cinématique, Dunod (Paris), 1968
Voir aussi
Lien externe
- Torseur - SciencesIndustrielles.com
Bibliographie
- Michel Combarnous, Didier Desjardins et Christophe Bacon, Mécanique des solides et des systèmes de solides, Dunod, coll. « Sciences sup », , 3e éd. (ISBN 978-2-10-048501-7), p. 109-118
- Jean-Louis Fanchon, Guide de mécanique, Nathan, , 543 p. (ISBN 978-2-09-178965-1), p. 105-116
- P.Brousse, Cours de mécanique, 1er cycle et classes préparatoires aux grandes écoles scientifiques, Armand Colin collection U























































