Cet article est une ébauche concernant la géométrie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
La mise en forme de cet article est à améliorer ().
La mise en forme du texte ne suit pas les recommandations de Wikipédia : il faut le « wikifier ».
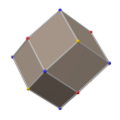
| Octangle étoilé | |
|---|---|
| |
| Type | Stellation et composé |
| Polyèdres | 2 tétraèdres |
| Faces | 8 triangles |
| Arêtes | 12 |
| Sommets | 8 |
| Groupe de symétrie | octaédrique (Oh) |
L'octangle étoilé est un composé polyédrique aussi connu sous le nom de stella octangula, d'octaèdre étoilé, d'étoile à huit pointes, ou encore d'étoile de David à trois dimensions. Il a été mentionné en 1509 par Luca Pacioli dans son livre « de divina proportione », puis redécouvert par Johannes Kepler en 1609, qui le baptisa stella octangula (étoile à huit sommets).
C'est le plus simple des cinq composés polyédriques réguliers, et le seul composé régulier de deux tétraèdres.
- Projections orthographiques
-
-
-
Il peut être vu soit comme composé polyédrique, soit comme stellation.
Comme composé, c'est la réunion de deux tétraèdres. Les sommets des deux tétraèdres sont ceux d'un cube. L'intersection des deux solides tétraédriques est un octaèdre dont les faces sont incluses dans celles du composé. L'octangle peut donc être vu comme un octaèdre sur les faces duquel ont été posées des pyramides. Il a la même topologie que le solide de Catalan convexe nommé triakioctaèdre, qui possède de plus petites pyramides.
Comme stellation, c'est la seule extension étoilée de l'octaèdre. Chaque face triangulaire de l'octaèdre est remplacée par le triangle équilatéral dont les milieux des côtés sont les sommets de cette face (voir le modèle W19 de Wenninger dans la liste des polyèdres de Wenninger (en)).
-
Premier tétraèdre... -
...et son dual. -
Octaèdre intersection. -
Enveloppe convexe des sommets.
-
Si les 6 points de croisements des arêtes étaient aussi marqués comme sommets... -
...la projection sur la sphère circonscrite serait la même que celle d'un dodécaèdre rhombique.
L'octangle dans l'art
[modifier | modifier le code]L'octangle étoilé apparaît en compagnie d'autres polyèdres et composés polyédriques dans la lithographie "Étoiles" de M. C. Escher et en constitue la forme centrale dans "Double Planétoïde" .
Références
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Stellated octahedron » (voir la liste des auteurs).
- (en) Peter R. Cromwell, Polyhedra, Cambridge, 1997
