| Prisme pentagrammique uniforme | |
| |
| Type | Polyèdre semi-régulier |
|---|---|
| Éléments | F=7, A=15, S=10 (χ=2) |
| Faces par côtés | 5{4}+2{5/2} |
| Symbole de Schläfli | t{2,5/2} |
| Symbole de Wythoff | 2 5/2 | 2 |
| Coxeter-Dynkin | |
| Symétrie | D5h (en) |
| Références | U78(a) |
| Dual | Bipyramide pentagrammique |
| Propriétés | convexe |
 Configuration de sommet 4.4.5/2 | |
| modifier |
|
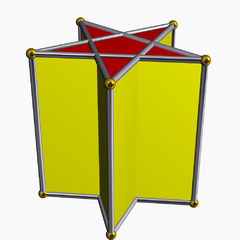
En géométrie, le prisme pentagrammique est un élément de l'ensemble infini des prismes non-convexes formés par des côtés carrés et deux polygones étoilés réguliers, dans ce cas, deux pentagrammes.
Ce polyèdre uniforme est indexé sous le nom U78.
C'est un cas particulier d'un prisme droit avec une base pentagrammique, qui en général, a des faces de côté rectangulaires.
NOTE : Les faces pentagrammiques ont un intérieur ambigu parce qu'il s'auto-coupe. La région pentagonale centrale peut être considérée intérieure ou extérieure, dépendant de la manière dont l'intérieur est défini. Une définition de l'intérieur est l'ensemble des points qui ont un segment qui croise la frontière un nombre impair de fois pour échapper au périmètre.
Dans les deux cas, il est meilleur de montrer la frontière pentagrammique pour le distinguer d'un décagone concave.
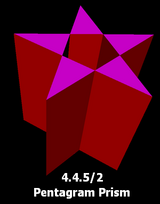
Une représentation alternative avec des centres creux dans les pentagrammes.
Liens externes
- http://www.mathconsult.ch/showroom/unipoly/78.html
- http://bulatov.org/polyhedra/uniform/u03.html
- http://home.aanet.com.au/robertw/Prism52.html
- http://www.math.technion.ac.il/~rl/kaleido/data/03.html
- http://home.comcast.net/~tpgettys/nonconvexprisms.html
- https://web.archive.org/web/20060211140715/http://www.ac-noumea.nc/maths/amc/polyhedr/no_conv5_.htm
- Patron en papier d'un prisme pentagonal








