On appelle fluide newtonien (en hommage à Isaac Newton) un fluide dont la loi contrainte – vitesse de déformation est linéaire[1],[2],[3]. La constante de proportionnalité est appelée viscosité.
Définition
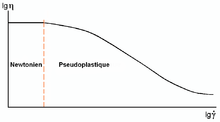
Viscosité et cisaillement
L’équation décrivant le « comportement newtonien » en description eulérienne est :
où :
- est la contrainte de cisaillement exercée par le fluide (à l'origine des forces de traînée), exprimée en Pa ;
- est la viscosité dynamique du fluide — une constante de proportionnalité caractéristique du matériau, en Pa s ;
- est le gradient de vitesse perpendiculaire à la direction de cisaillement, en s−1.
En termes usuels, cela signifie que le fluide continue de s’écouler indépendamment des forces extérieures qui agissent sur lui. Par exemple, l’eau est un fluide newtonien parce qu’elle continue d’exhiber les propriétés d’un fluide quelle que soit la vitesse à laquelle elle est agitée. Les solutions aqueuses et les huiles de faible viscosité, la plupart des solvants, l’air, de nombreux gaz, sont des exemples de fluides newtoniens. Pour un fluide newtonien, la viscosité, par définition, ne dépend que de la température (la viscosité d'un liquide diminue à mesure que la température augmente)[4] et de la pression (mais elle dépend aussi de la composition chimique du fluide si ce n'est pas un corps pur), non des forces agissant sur l'élément de fluide.
Dans un fluide non newtonien, la mise en rotation provoque soit l’apparition d’un creux (qui se comble graduellement au fil du temps ; on voit ce comportement dans les crèmes, les suspensions d’amidon et les plastisols PVC, ou, rigueur mise à part, dans les limons), soit une ascension du fluide autour de l’agitateur (phénomène dit « effet Weissenberg ») à cause de la thixotropie, la variation brutale de viscosité se traduisant par une propension accrue à l'écoulement (on observe ce phénomène dans les peintures dites « sans tache », qu'il est facile d'étaler mais qui sont plus visqueuses sur un mur).
Composante sphérique des contraintes
La notion de fluide newtonien ne décrit que les effets de cisaillement dans le fluide. Il importe de comprendre que la seule précision de « newtonien » ne suffit pas à caractériser la loi de comportement du fluide : il faut y adjoindre les effets de compressibilité.
Si le fluide est compressible et que la viscosité est uniforme dans le fluide, en utilisant la convention de sommation d'Einstein, on a :
Si le fluide est incompressible et que la viscosité est uniforme dans le fluide, l’équation donnant la loi de comportement, en description eulérienne et en coordonnées cartésiennes, est :
Naturellement, tous les fluides réels sont plus ou moins compressibles.
Un autre tenseur, (aussi noté ), représentant la contrainte totale, s'exprime en combinant la contrainte de cisaillement avec la pression conventionnelle (thermodynamique) :
où, selon la convention tensorielle :
- est la contrainte de cisaillement sur la -ième facette d'un élément de fluide dans la -ème direction ;
- est la pression thermodynamique ;
- est la vitesse dans la -ième direction ;
- est la -ème direction coordonnée.
Tout fluide ne respectant pas cette loi est dit non newtonien : il existe différents liquides de ce type, notamment les polymères fondus, le sang, les gels, les boues, les pâtes, les suspensions, les émulsions, certaines solutions solides et la plupart des fluides fortement visqueux.
Seconde viscosité
La seconde viscosité participe à la caractérisation totale du fluide newtonien isotrope. C'est un paramètre théorique important souvent omis. Néanmoins la définition de l'IUPAC[5] est très claire sur ce point, la définition d'un fluide newtonien comporte deux paramètres.
Un paradoxe classique est alors de constater que les deux définitions du fluide newtonien sont contradictoires : celle sur la proportionnalité implique deux paramètres et relève de l'algèbre linéaire ; celle sur la caractérisation par la seule viscosité principale n'utilise qu'un paramètre.
Le paradoxe disparait quand on décide de préciser que la vitesse de déformation est soit la vitesse de la déformation totale, soit la vitesse du seul changement de forme.
Anisotropie
Comme pour la seconde viscosité, la définition du fluide newtonien par la linéarité n'exclut pas que le fluide soit anisotrope.
La viscosité est alors décrite par un tenseur .
Applications
Le modèle du fluide newtonien joue un rôle central en mécanique des fluides, puisqu'hormis le modèle du fluide parfait incompressible, il fournit le modèle le plus simple de comportement fluide. L'hypothèse de fluide newtonien est à la base :
- des équations de Navier-Stokes ;
- de la solution de Poiseuille pour l'écoulement laminaire des fluides visqueux.
Références
- Armando Lencastre (trad. du portugais), Hydraulique générale, Paris/s.l., Eyrolles, (réimpr. 1983, 1995), 636 p. (ISBN 2-212-01894-0), « 4 - Écoulements en régime permanent »
- Inge L. Rhyming, Dynamique des fluides, Presses polytechniques romandes, (réimpr. 1985, 1991), 462 p. (ISBN 2-88074-224-2), « Chapitre 6 - Écoulement des fluides visqueux incompressibles », p. 197
- Paul Germain, Mécanique des milieux continus, vol. 1 : Concepts généraux, Masson & Cie, , 418 p. (ISBN 978-2-7302-1245-8, lire en ligne), « VI-2. Fluides », p. 125
- (en-US) Mohammad, « Newtonian Fluids - Definition and The Viscosity », sur Pharmatech, (consulté le )
- (en) « Newtonian fluid », IUPAC, Compendium of Chemical Terminology [« Gold Book »], Oxford, Blackwell Scientific Publications, 1997, version corrigée en ligne : (2019-), 2e éd. (ISBN 0-9678550-9-8)
Annexes
Articles connexes
Bibliographie
- Paul Germain, Mécanique des milieux continus, vol. 1 : Concepts généraux, Masson & Cie, , 418 p. (ISBN 978-2-7302-1245-8, lire en ligne)
- J. Lemaitre J.-L. Chaboche, Mécanique des matériaux solides, Paris, Dunod, , 544 p. (ISBN 2-04-018618-2)
- Inge L. Rhyming, Dynamique des fluides, Presses polytechniques romandes, (réimpr. 1985,1991), 462 p. (ISBN 2-88074-224-2), « Chapitre 6 - Écoulement des fluides visqueux incompressibles », p. 197
- E. Guyon, J.-P. Hulin et L. Petit, Hydrodynamique Physique, CNRS Éditions, , 673 p.
























