Loi log-Laplace
Densité de probabilité de la loi à trois paramètres
Fonction de répartition de la loi à trois paramètres
Paramètres	${\displaystyle \mu >0}$ paramètre de position ${\displaystyle b>0\,}$ paramètre d'échelle
Support	${\displaystyle x\in ]0,+\infty [\!}$
Densité de probabilité	${\displaystyle {\frac {1}{2bx}}\exp \left(-{\frac {|\mu -\ln x|}{b}}\right)}$
Fonction de répartition	${\displaystyle {\frac {1}{4bx}}[1+\operatorname {sgn}(\log(y)-\mu )\,(1-e^{-{\frac {|\log(y)-\mu |}{b}}})]}$
Fonction caractéristique	pas de forme explicite
modifier

En théorie des probabilités et en statistique, la loi log-Laplace est la loi de probabilité continue d'une variable aléatoire dont le logarithme suit une loi de Laplace.

Autrement dit, Si X suit une loi de Laplace avec paramètres ${\displaystyle \mu }$ et b, alors ${\displaystyle Y=\exp(X)}$ suit une loi log-Laplace. Les propriétés sont ainsi issues de celles de la loi de Laplace.

Une généralisation possible de cette loi est d'introduire un nouveau paramètre, c'est la loi log-Laplace à trois paramètres.

Si X suit une loi log-Laplace, on notera ${\displaystyle X\sim LL(\mu ,b)}$ ou ${\displaystyle X\sim LL(\delta ,\alpha ,\beta )}$.

La densité de probabilité de la loi log-Laplace avec paramètres ${\displaystyle \mu }$ et b est donnée par^[1] :

${\displaystyle f(x|\mu ,b)={\begin{cases}{\frac {1}{2bx}}\exp \left(-{\frac {|\ln x-\mu |}{b}}\right)&{\text{ si }}x>0\\0&{\text{ sinon}}\end{cases}}}$

${\displaystyle ={\begin{cases}{\frac {1}{2bx}}\exp \left(-{\frac {\mu -\ln x}{b}}\right)&{\text{ pour }}x>0{\text{ et si }}x<e^{\mu }\\{\frac {1}{2bx}}\exp \left(-{\frac {\ln x-\mu }{b}}\right)&{\text{ pour }}x>0{\text{ et si }}x\geq e^{\mu }\\0&{\text{ pour }}x<0.\end{cases}}}$

Par les changements de variables : ${\displaystyle \delta =e^{\mu }}$ et ${\displaystyle \beta ={\frac {1}{b}}-1}$, la densité s'écrit sous le forme obtient :

${\displaystyle f(x|\delta ,\beta )={\begin{cases}{\frac {1}{\delta }}{\frac {\beta }{2}}\left({\frac {x}{\delta }}\right)^{\beta -1}&{\text{ si }}0<x<\delta \\{\frac {1}{\delta }}{\frac {\beta }{2}}\left({\frac {\delta }{x}}\right)^{\beta +1}&{\text{ si }}\delta <x\end{cases}}}$

La fonction de répartition de la loi log-Laplace de paramètres ${\displaystyle \mu }$ et b est donnée par :

${\displaystyle F(y)={\begin{cases}{\frac {1}{4bx}}\left[1+\operatorname {sgn}(\log(y)-\mu )\,(1-e^{-{\frac {|\log(y)-\mu |}{b}}})\right]&{\text{ si }}x>0\\0&{\text{ sinon.}}\end{cases}}}$

En fonction des paramètres, la loi log-Laplace peut ou peut ne pas avoir de moyenne finie et de variance finie^[2].

Il existe la généralisation^[2] suivante de la loi log-Laplace incluant un nouveau paramètre, c'est la loi log-Laplace à trois paramètres définie par la densité de probabilité :

${\displaystyle f(x|\delta ,\alpha ,\beta )={\begin{cases}0&{\text{ si }}x<0\\{\frac {1}{\delta }}{\frac {\alpha \beta }{\alpha +\beta }}\left({\frac {x}{\delta }}\right)^{\beta -1}&{\text{ si }}0<x<\delta \\{\frac {1}{\delta }}{\frac {\alpha \beta }{\alpha +\beta }}\left({\frac {\delta }{x}}\right)^{\alpha +1}&{\text{ si }}\delta <x\end{cases}}}$

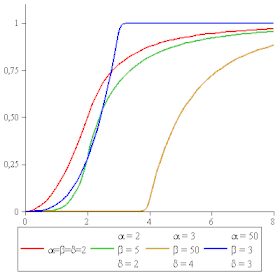
avec ${\displaystyle \alpha >0}$, ${\displaystyle \beta >0}$, ${\displaystyle \delta >0}$. La fonction de répartition de la loi log-Laplace à trois paramètres est

${\displaystyle F(y|\delta ,\alpha ,\beta )={\begin{cases}0&{\text{ si }}y<0\\{\frac {\alpha }{\alpha +\beta }}\left({\frac {x}{\delta }}\right)^{\beta }&{\text{ si }}0<x<\delta \\1-{\frac {\beta }{\alpha +\beta }}\left({\frac {\delta }{x}}\right)^{\alpha }&{\text{ si }}\delta <x.\end{cases}}}$

• Si ${\displaystyle Y\sim LL(\delta ,\alpha ,\beta )}$, alors pour tout ${\displaystyle c>0}$, ${\displaystyle cY\sim LL(c\delta ,\alpha ,\beta )}$,
• Si ${\displaystyle Y\sim LL(\delta ,\alpha ,\beta )}$, alors, ${\displaystyle {\frac {1}{Y}}\sim LL({\frac {1}{\delta }},\alpha ,\beta )}$

• ${\displaystyle LL(1,\infty ,\beta ):=\lim _{\alpha \rightarrow \infty }LL(1,\alpha ,\beta )\sim \mathrm {Beta} (\beta )}$ (loi bêta),
• ${\displaystyle LL(1,\alpha ,\infty ):=\lim _{\beta \rightarrow \infty }LL(1,\alpha ,\beta )\sim \mathrm {Pareto} (\alpha )}$ (distribution de Pareto).

La loi log-Laplace est, par exemple, utilisée pour modéliser la forme de la densité de la température de l'air. Des études du climat de la ville islandaise de Stykkishólmur ont été réalisées et la loi log-Laplace a été utilisée ; plus particulièrement en mélangeant deux lois log-Laplace tronquées^[3].

Cette loi est également appliquée dans d'autres domaines^[2] : échanges commerciaux, tailles d'entreprise, etc.

• Portail des probabilités et de la statistique