Loi de Fréchet
Densité de probabilité
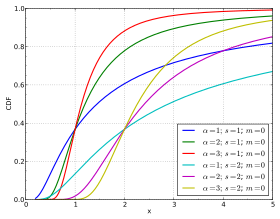
Fonction de répartition
Paramètres
α
∈
]
0
,
∞
[
{\displaystyle \alpha \in ]0,\infty [}
paramètre de forme .
s
∈
]
0
,
∞
[
{\displaystyle s\in ]0,\infty [}
paramètre d'échelle (par défaut :
s
=
1
{\displaystyle s=1\,}
m
∈
]
−
∞
,
∞
[
{\displaystyle m\in ]-\infty ,\infty [}
paramètre de position du minimum (par défaut :
m
=
0
{\displaystyle m=0\,}
Support
x
>
m
{\displaystyle x>m}
Densité de probabilité
α
s
(
x
−
m
s
)
−
1
−
α
e
−
(
x
−
m
s
)
−
α
{\displaystyle {\frac {\alpha }{s}}\;\left({\frac {x-m}{s}}\right)^{-1-\alpha }\;\mathrm {e} ^{-({\frac {x-m}{s}})^{-\alpha }}}
Fonction de répartition
e
−
(
x
−
m
s
)
−
α
{\displaystyle \mathrm {e} ^{-({\frac {x-m}{s}})^{-\alpha }}}
Espérance
{
m
+
s
Γ
(
1
−
1
α
)
pour
α
>
1
∞
sinon
{\textstyle {\begin{cases}\ m+s\Gamma \left(1-{\frac {1}{\alpha }}\right)&{\text{pour }}\alpha >1\\\ \infty &{\text{sinon}}\end{cases}}}
Médiane
m
+
s
ln
(
2
)
α
{\displaystyle m+{\frac {s}{\sqrt[{\alpha }]{\ln(2)}}}}
Mode
m
+
s
(
α
1
+
α
)
1
/
α
{\displaystyle m+s\left({\frac {\alpha }{1+\alpha }}\right)^{1/\alpha }}
Variance
{
s
2
(
Γ
(
1
−
2
α
)
−
(
Γ
(
1
−
1
α
)
)
2
)
pour
α
>
2
∞
sinon
{\textstyle {\begin{cases}s^{2}\left(\Gamma \left(1-{\frac {2}{\alpha }}\right)-\left(\Gamma \left(1-{\frac {1}{\alpha }}\right)\right)^{2}\right)&{\text{pour }}\alpha >2\\\ \infty &{\text{sinon}}\end{cases}}}
Asymétrie
voir l'article
Kurtosis normalisé
voir l'article
Entropie
1
+
γ
α
+
γ
+
ln
(
s
α
)
{\displaystyle 1+{\frac {\gamma }{\alpha }}+\gamma +\ln \left({\frac {s}{\alpha }}\right)}
γ
{\displaystyle \gamma }
constante d'Euler-Mascheroni .
Fonction génératrice des moments
le k -ième moment existe[ 1]
α
>
k
{\displaystyle \alpha >k}
Fonction caractéristique
voir Muraleedharan, Soares & Lucas (2011)[ 1]
modifier
En théorie des probabilités et en statistique , la loi de Fréchet est un cas particulier de loi d'extremum généralisée au même titre que la loi de Gumbel ou la loi de Weibull .
Le nom de cette loi est dû à Maurice Fréchet , auteur d'un article à ce sujet en 1927. Des travaux ultérieurs ont été réalisés par Ronald Aylmer Fisher et L. H. C. Tippett en 1928 et par Emil Julius Gumbel en 1958.
Sa fonction de répartition est donnée par :
P
(
X
≤
x
)
=
{
1
−
e
−
x
−
α
si
x
>
0
0
sinon
{\displaystyle \mathbb {P} (X\leq x)={\begin{cases}1-\mathrm {e} ^{-x^{-\alpha }}&{\text{ si }}x>0\\0&{\text{ sinon}}\end{cases}}}
où
α
>
0
{\displaystyle \alpha >0}
paramètre de forme . Cette loi peut être généralisée en introduisant un paramètre de position m du minimum et un paramètre d'échelle s >0. La fonction de répartition est alors :
P
(
X
≤
x
)
=
{
1
−
e
−
(
x
−
m
s
)
−
α
si
x
>
m
0
sinon.
{\displaystyle \mathbb {P} (X\leq x)={\begin{cases}1-\mathrm {e} ^{-\left({\frac {x-m}{s}}\right)^{-\alpha }}&{\text{ si }}x>m\\0&{\text{ sinon.}}\end{cases}}}
La loi de Fréchet de paramètre
α
{\displaystyle \alpha }
moments standards :
μ
k
=
∫
0
∞
x
k
f
(
x
)
d
x
=
∫
0
∞
t
−
k
α
e
−
t
d
t
{\displaystyle \mu _{k}=\int _{0}^{\infty }x^{k}f(x)\mathrm {d} x=\int _{0}^{\infty }t^{-{\frac {k}{\alpha }}}\mathrm {e} ^{-t}\mathrm {d} t}
(avec
t
=
x
−
α
{\displaystyle t=x^{-\alpha }}
k
<
α
{\displaystyle k<\alpha }
μ
k
=
Γ
(
1
−
k
α
)
{\displaystyle \mu _{k}=\Gamma \left(1-{\frac {k}{\alpha }}\right)}
où
Γ
(
z
)
{\displaystyle \Gamma (z)}
fonction Gamma .
En particulier :
Pour
α
>
1
{\displaystyle \alpha >1}
espérance est
E
[
X
]
=
Γ
(
1
−
1
α
)
{\displaystyle \mathbb {E} [X]=\Gamma (1-{\tfrac {1}{\alpha }})}
Pour
α
>
2
{\displaystyle \alpha >2}
variance est
Var
(
X
)
=
Γ
(
1
−
2
α
)
−
(
Γ
(
1
−
1
α
)
)
2
{\textstyle {\text{Var}}(X)=\Gamma (1-{\frac {2}{\alpha }})-\left(\Gamma (1-{\frac {1}{\alpha }})\right)^{2}}
Le quantile
q
y
{\displaystyle q_{y}}
y
{\displaystyle y}
q
y
=
F
−
1
(
y
)
=
(
−
ln
y
)
−
1
α
{\displaystyle q_{y}=F^{-1}(y)=(-\ln y)^{-{\frac {1}{\alpha }}}}
En particulier la médiane est :
q
1
/
2
=
(
ln
2
)
−
1
α
{\displaystyle q_{1/2}=(\ln 2)^{-{\frac {1}{\alpha }}}}
Le mode de la loi de Fréchet est
(
α
α
+
1
)
1
α
{\displaystyle \left({\frac {\alpha }{\alpha +1}}\right)^{\frac {1}{\alpha }}}
Pour la loi de Fréchet à trois paramètres, le premier quartile est
q
1
=
m
+
s
ln
(
4
)
α
{\textstyle q_{1}=m+{\frac {s}{\sqrt[{\alpha }]{\ln(4)}}}}
q
3
=
m
+
s
ln
(
4
3
)
α
{\textstyle q_{3}=m+{\frac {s}{\sqrt[{\alpha }]{\ln \left({\frac {4}{3}}\right)}}}}
L'asymétrie de la loi de Fréchet est :
{
Γ
(
1
−
3
α
)
−
3
Γ
(
1
−
2
α
)
Γ
(
1
−
1
α
)
+
2
Γ
3
(
1
−
1
α
)
(
Γ
(
1
−
2
α
)
−
Γ
2
(
1
−
1
α
)
)
3
pour
α
>
3
∞
sinon
{\displaystyle {\begin{cases}\ {\frac {\Gamma \left(1-{\frac {3}{\alpha }}\right)-3\Gamma \left(1-{\frac {2}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+2\Gamma ^{3}\left(1-{\frac {1}{\alpha }}\right)}{\sqrt {\left(\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right)^{3}}}}&{\text{pour }}\alpha >3\\\ \infty &{\text{sinon}}\end{cases}}}
le kurtosis est :
{
−
6
+
Γ
(
1
−
4
α
)
−
4
Γ
(
1
−
3
α
)
Γ
(
1
−
1
α
)
+
3
Γ
2
(
1
−
2
α
)
[
Γ
(
1
−
2
α
)
−
Γ
2
(
1
−
1
α
)
]
2
pour
α
>
4
∞
sinon
{\displaystyle {\begin{cases}\ -6+{\frac {\Gamma \left(1-{\frac {4}{\alpha }}\right)-4\Gamma \left(1-{\frac {3}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+3\Gamma ^{2}\left(1-{\frac {2}{\alpha }}\right)}{\left[\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right]^{2}}}&{\text{pour }}\alpha >4\\\ \infty &{\text{sinon}}\end{cases}}}
Loi de Fréchet utilisée pour modéliser des précipitations extrêmes. En hydrologie , la loi de Fréchet s'utilise pour des évènements extrêmes tels que le maximum annuel des précipitations journalières ou le débit des rivières[ 2] Oman , montrant également la bande de confiance de 90 % basée sur la loi binomiale .
Si
X
∼
U
(
0
,
1
)
{\displaystyle X\sim U(0,1)\,}
loi uniforme continue ) alors
m
+
s
(
−
log
(
X
)
)
−
1
/
α
∼
Frechet
(
α
,
s
,
m
)
{\displaystyle m+s(-\log(X))^{-1/\alpha }\sim {\textrm {Frechet}}(\alpha ,s,m)\,}
Si
X
∼
Frechet
(
α
,
s
,
m
)
{\displaystyle X\sim {\textrm {Frechet}}(\alpha ,s,m)\,}
k
X
+
b
∼
Frechet
(
α
,
k
s
,
k
m
+
b
)
{\displaystyle kX+b\sim {\textrm {Frechet}}(\alpha ,ks,km+b)\,}
Si
X
i
=
Frechet
(
α
,
s
,
m
)
{\displaystyle X_{i}={\textrm {Frechet}}(\alpha ,s,m)\,}
Y
=
max
{
X
1
,
…
,
X
n
}
{\displaystyle Y=\max\{\,X_{1},\ldots ,X_{n}\,\}\,}
Y
∼
Frechet
(
α
,
n
1
α
s
,
m
)
{\displaystyle Y\sim {\textrm {Frechet}}(\alpha ,n^{\tfrac {1}{\alpha }}s,m)\,}
Si
X
∼
Weibull
(
k
=
α
,
λ
=
m
)
{\displaystyle X\sim {\textrm {Weibull}}(k=\alpha ,\lambda =m)\,}
loi de Weibull ) alors
m
2
X
∼
Frechet
(
α
,
s
,
m
)
{\displaystyle {\tfrac {m^{2}}{X}}\sim {\textrm {Frechet}}(\alpha ,s,m)\,}
↑ a et b (en) G. Muraleedharan, C. Guedes Soares et Cláudia Lucas, chap. 14 « Characteristic and Moment Generating Functions of Generalised Extreme Value Distribution (GEV) » , dans Linda L. Wright, Sea Level Rise, Coastal Engineering, Shorelines and Tides , Nova Science Publishers , 2011 (ISBN 978-1-61728-655-1 , p. 269-276 ↑ (en) Stuart Coles, An Introduction to Statistical Modeling of Extreme Values , Londres, Springer-Verlag , 2001 , 2e éd. , 208 p. (ISBN 978-1-85233-459-8 lire en ligne ) M. Fréchet, « Sur la loi de probabilité de l'écart maximum », Ann. Soc. Polon. Math. , vol. 6, no 3, 1927
(en) R. A. Fisher et L. H. C. Tippett, « Limiting forms of the frequency distribution of the largest and smallest member of a sample », Proc. Cambridge Phil. Soc. , vol. 24, 1928, p. 180-190 (en) E. J. Gumbel, Statistics of Extremes , Columbia University Press , New York, 1958(en) S. Kotz et S. Nadarajah, Extreme Value Distributions: Theory and Applications , World Scientific , 2000 (ISBN 1860942245 










![{\displaystyle \alpha \in ]0,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6872c362037ca2026acc725580468057792952f8)
![{\displaystyle s\in ]0,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fabdae1f19057f6387cf9bf99e90fb2c58ece116)

![{\displaystyle m\in ]-\infty ,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b9e8b374ecc87361d353bdc6b26ae13067b4a5d)





![{\displaystyle m+{\frac {s}{\sqrt[{\alpha }]{\ln(2)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4bbcc7e1ba7727e7f224dd9f74d315568646250)















![{\displaystyle \mathbb {E} [X]=\Gamma (1-{\tfrac {1}{\alpha }})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93643892310f43b1dcc028bb34e9282b89207ec7)







![{\textstyle q_{1}=m+{\frac {s}{\sqrt[{\alpha }]{\ln(4)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11d581fa6a82111ba1e1e028f73d2621142ed578)
![{\textstyle q_{3}=m+{\frac {s}{\sqrt[{\alpha }]{\ln \left({\frac {4}{3}}\right)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8d86a23c4e23c309c5da4242dc9edbbca0fc2ec)

![{\displaystyle {\begin{cases}\ -6+{\frac {\Gamma \left(1-{\frac {4}{\alpha }}\right)-4\Gamma \left(1-{\frac {3}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+3\Gamma ^{2}\left(1-{\frac {2}{\alpha }}\right)}{\left[\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right]^{2}}}&{\text{pour }}\alpha >4\\\ \infty &{\text{sinon}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4a0b46e0c4dcfc7ccb163ec376647482c3f6d472)








