En géométrie, un problème de construction d'un triangle est la recherche d'une construction à la règle et au compas d'un triangle à partir de trois éléments caractéristiques donnés (des longueurs ou des points : sommets ou centres de ce triangle).

La construction de triangles à partir de longueurs de côtés et de mesures d'angles données sont classiques.

On compte six problèmes dont la solution est "unique" dans le sens où elle donne des triangles isométriques^[1],[2]:

• SSS (side, side, side), avec les trois longueurs de côtés données
• SAS (side, angle, side), avec deux longueurs de côtés et l'angle formé par ceux-ci donnés
• ASA (angle, side, angle), avec une longueur de côté et les deux angles aux deux extrémités
• AAS (angle, angle, side), avec une longueur de côté, un angle à une des deux extrémités, et l'angle au 3^e sommet du triangle
• HL (hypotenuse, leg), qui vise à construire un triangle rectangle à partir de son hypoténuse et d'un des côtés.

• 
  Cas d'isométrie SSS
• 
  Cas d'isométrie SAS
• 
  Cas d'isométrie ASA
• 
  Cas d'isométrie AAS

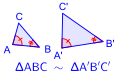
La configuration AAA ne permet que d'obtenir des triangles semblables.

• 
  Configuration AAA : les deux triangles sont semblables, mais non isométriques.

La configuration SSA ne suffit pas pour déterminer des triangles isométriques, il faut pour cela ajouter une condition sur la nature acutangle ou obtusangle du triangle^[2].

• 
  Dans la configuration SSA, deux triangles non semblables peuvent être solutions.

D'autres problèmes prennent comme données possibles les longueurs des médianes, des hauteurs, des segments internes des bissectrices, le rayon du cercle circonscrit ou du cercle inscrit, ou encore le demi-périmètre .

En prenant un triplet de données parmi les longueurs, les mesures d'angles et les longueurs données ci-dessus, on atteint ${\textstyle {\binom {18}{3}}=816}$ problèmes dont 186 non-triviaux^[3].

En utilisant les notations suivantes, Wernick considère les triplets de points parmi :

• les sommets A, B, C et le centre du cercle circonscrit O
• les milieux des côtés M_a, M_b, M_c et le centre de gravité G
• les pieds des hauteurs H_a, H_b, H_c et l'orthocentre H
• les pieds des bissectrices (internes) T_a, T_b, T_c et le centre du cercle inscrit I

Il existe alors ${\textstyle {\binom {16}{3}}=560}$ triplets possibles mais seulement 139 cas non triviaux, en enlevant les cas symétriques (les triplets (A, B, M_a) et (B, C, M_c) par exemple).

Wernick les sépare en quatre catégories :

• R pour redundant : un des points du triplet est constructible à partir des deux autres. Le problème n'a alors aucune solution.
• L pour locus : il n'existe pas de solution unique au problème mais un ensemble de solutions infini (une droite, un cercle).
• S pour solvable : le triangle peut être construit à la règle et au compas (la méthode de construction n'est pas forcément connue).
• U pour unsolvable ou unclassified : le triangle solution ne peut pas être construit à la règle et au compas ou le problème de la construction reste ouvert.

En 2012, on compte 72 problèmes classés S, 16 problèmes classés U, 3 classés R et 23 problèmes classés L.

Exemples

• Un problème S simple est celui du triplet (A, B, G) , qui se résout comme suit :
  • Tracer le milieu de [AB], qui est M_c
  • Tracer le point C qui vérifie ${\displaystyle {\overrightarrow {GC}}=2{\overrightarrow {M_{c}G}}}$
• Un problème S dont la solution n'est pas connue est le triplet (H, T_a, I).
• Un problème L simple est celui du triplet (A, B, O), car tout point C sur le cercle de centre O et passant par A (et donc B) est solution
• Les trois problèmes R sont redondants :
  • (A, B, M_c) sont tous trois sur le même côté du triangle
  • (A, M_a, G) sont tous trois sur une même médiane
  • (O, G, H) sont tous trois sur la droite d'Euler du triangle
• Un problème U prouvé comme irrésoluble est celui lié au triplet (A, G, T_c).

Aux points choisis par Wernick, Connelly ajoute le centre du cercle d'Euler N et les « points d'Euler » E_a, E_b, E_c (les intersections des hauteurs et du cercle d'Euler, soit les milieux des segments joignant les sommets et l'orthocentre).

Ce compendium apporte donc ${\textstyle {\binom {20}{3}}=1140}$ triplets possibles, dont 113 non triviaux : 73 problèmes classés S, 16 problèmes classés U, 5 classés R et 19 problèmes L.

• (en) « On-line compendiums of triangle location construction problems »
• (en) William Wernick, « Triangle Constructions with Three Located Points », Mathematics Magazine, vol. 55, n^o 4,‎ 1982.
• (en) Leroy F. Meyers, « Update on William Wernick's "Triangle Constructions with Three Located Points" », Mathematics Magazine, Taylor & Francis, Ltd., vol. 69, n^o 1,‎ février 1996, p. 46-49 (DOI 10.2307/2691396, JSTOR 2691396)
• (en) Harold Connelly, « An Extension of Triangle Constructions from Located Points », Forum Geometricorum, vol. 9,‎ 2009 (lire en ligne).
• (en) Vesna Marinkovic et Predrag Janicic, « Towards Understanding Triangle Construction Problems », Intelligent Computer Mathematics - CICM 2012. Lecture Notes in Computer Science, Springer, vol. 7362,‎ 2012 (lire en ligne).
• (en) Vesna Marinkovic, Pascal Schreck et Predrag Janicic, « Computer Theorem Proving for Verifiable Solving of Geometric Construction Problems », Automated Deduction in Geometry 2014, LNCS 9201, Springer,‎ 2015 (lire en ligne).
• (en) Vesna Marinkovic, « ArgoTriCS - Automated Triangle Construction Solver », Journal of Experimental and Theoretical Artificial Intelligence, vol. 29, n^o 2,‎ 2007, p. 247-271 (DOI 10.1080/0952813X.2015.1132271).

• Résolution d'un triangle
• Triangles isométriques

• Portail de la géométrie